Question

选修4-5：不等式选讲
已知函数f（x）=|2x+1|-|x-3|．
（Ⅰ）解不等式f（x）≤4；
（Ⅱ）若存在x使得f（x）+a≤0成立，求实数a的取值范围．

Answer 1

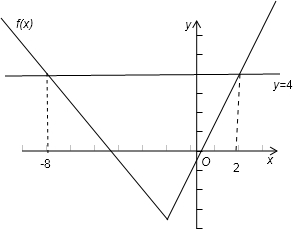
分析：（Ⅰ）化简f（x）的解析式，并画出图象，找出与y=4的交点，从而得到不等式f（x）≤4的解集．
（Ⅱ）由f（x）的图象知，x=-

1

2

时，f（x）有最小值-

7

2

，由题意知，实数a大于或等于f（x）的最小值．

解答：解：（Ⅰ）f（x）=|2x+1|-|x-3|=

-x-4  ，(x≤- 1 2 ) 3x-2  ，(- 1 2 ≤x＜3 ) x+4  ，(x≥3)

，如图，它与 y=4的交点为（-8，4）和（2，4）．
故不等式f（x）≤4的解集为[-8，2]．
（Ⅱ）由f（x）的图象知，x=-

1

2

时，f（x）有最小值-

7

2

，存在x使得f（x）+a≤0成立，
等价于-a≥-

7

2

，a≤

7

2

．故实数a的取值范围为（-∞，

7

2

）．

点评：本题考查绝对值不等式的解法，体现了数形结合的数学思想，画出函数图象是解题的关键．