
【题目】过抛物线![]() 的焦点
的焦点![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,抛物线在
两点,抛物线在![]() 处的切线交于
处的切线交于![]() .
.
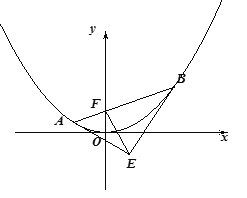
(1)求证:![]() ;
;
(2)设![]() ,当
,当![]() 时,求
时,求![]() 的面积
的面积![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】祖暅是我国古代的伟大科学家,他在5世纪末提出祖暅:“幂势即同,则积不容异”,意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意一个平面所截,若截面面积都相等,则这两个几何体的体积相等. 祖暅原理常用来由已知几何体的体积推导未知几何体的体积,例如由圆锥和圆柱的的体积推导半球体的体积,其示意图如图所示,其中图(1)是一个半径为R的半球体,图(2)是从圆柱中挖去一个圆锥所得到的几何体. (圆柱和圆锥的底面半径和高均为R)

利用类似的方法,可以计算抛物体的体积:在x-O-y坐标系中,设抛物线C的方程为y=1-x2 (-1![]() x
x![]() 1),将曲线C围绕y轴旋转,得到的旋转体称为抛物体. 利用祖暅原理可计算得该抛物体的体积为_________.
1),将曲线C围绕y轴旋转,得到的旋转体称为抛物体. 利用祖暅原理可计算得该抛物体的体积为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点
的焦点![]() 作直线
作直线![]() 与抛物线交于点
与抛物线交于点![]() 、
、![]() .
.
(1)求证:![]() 不是直角三角形.
不是直角三角形.
(2)当![]() 的斜率为
的斜率为![]() 时,抛物线上是否存在点
时,抛物线上是否存在点![]() ,使
,使![]() 为直角三角形?若存在,求出所有的点
为直角三角形?若存在,求出所有的点![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第35届牡丹花会期间,我班有5名学生参加志愿者服务,服务场所是王城公园和牡丹公园.
(1)若学生甲和乙必须在同一个公园,且甲和丙不能在同一个公园,则共有多少种不同的分配方案?
(2)每名学生都被随机分配到其中的一个公园,设![]() 分别表示5名学生分配到王城公园和牡丹公园的人数,记
分别表示5名学生分配到王城公园和牡丹公园的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 且椭圆上存在一点
且椭圆上存在一点![]() ,满足
,满足![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() 分别是椭圆
分别是椭圆![]() 的左、右顶点,过
的左、右顶点,过![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,记直线
两点,记直线![]() 的交点为
的交点为![]() ,是否存在一条定直线
,是否存在一条定直线![]() ,使点
,使点![]() 恒在直线
恒在直线![]() 上?
上?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com