
如图,在四棱锥ABCD-PGFE中,底面ABCD是直角梯形,侧棱垂直于底面,AB//DC,∠ABC=45o,DC=1,AB=2,PA=1.
(Ⅰ)求PD与BC所成角的大小;
(Ⅱ)求证:BC⊥平面PAC;
(Ⅲ)求二面角A-PC-D的大小.
(1)60o
(2)根据题意,由于BC⊥AC,且有PA⊥BC,则可以根据线面垂直的判定定理来得到结论。
(3)60o
解析试题分析:(Ⅰ)取的AB中点H,连接DH,易证BH//CD,且BD="CD" 1分
所以四边形BHDC为平行四边形,所以BC//DH
所以∠PDH为PD与BC所成角2分
因为四边形,ABCD为直角梯形,且∠ABC=45o, 所以DA⊥AB
又因为AB=2DC=2,所以AD=1, 因为Rt△PAD、Rt△DAH、Rt△PAH都为等腰直角三角形,所以PD=DH=PH= ,故∠PDH=60o 4分
,故∠PDH=60o 4分
(Ⅰ)连接CH,则四边形ADCH为矩形, ∴AH=DC 又AB=2,∴BH=1
在Rt△BHC中,∠ABC=45o , ∴CH=BH=1,CB= ∴AD=CH=1,AC=
∴AD=CH=1,AC=
∴AC2+BC2=AB2 ∴BC⊥AC……6分 又PA平面ABCD∴PA⊥BC ……7分
∵PA∩AC=A∴BC⊥平面PAC 8分
(Ⅲ)如图,分别以AD、AB、AP为x轴,y轴,z轴建立空间直角坐标系,则由题设可知:
A(0,0,0),P(0,0,1),C(1,1,0),D(1,0,0),
∴ =(0,0,1),
=(0,0,1), =(1,1,-1) 9分
=(1,1,-1) 9分
设m=(a,b,c)为平面PAC的一个法向量, 则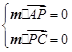 ,即
,即
设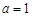 ,则
,则 ,∴m=(1,-1,0) 10分
,∴m=(1,-1,0) 10分
同理设n=(x,y,z) 为平面PCD的一个法向量,求得n=(1,1,1) 11分
∴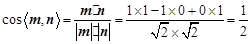 12分
12分
所以二面角A-PC-D为60o 13分
考点:空间角和距离的求解
点评:主要是考查了空间中线面角和二面角的平面角的求解,以及线面垂直的判定,属于基础题。


科目:高中数学 来源: 题型:解答题
如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2。将△ABD沿边AB折起, 使得△ABD与△ABC成30o的二面角 ,如图二,在二面角
,如图二,在二面角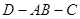 中.
中.
(1) 求CD与面ABC所成的角正弦值的大小;
(2) 对于AD上任意点H,CH是否与面ABD垂直。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知在四棱锥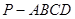 中,底面
中,底面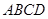 是边长为2的正方形,侧棱
是边长为2的正方形,侧棱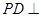 平面
平面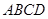 ,且
,且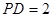 ,
, 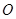 为底面对角线的交点,
为底面对角线的交点, 分别为棱
分别为棱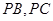 的中点
的中点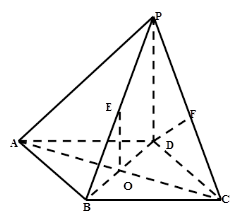
(1)求证: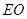 //平面
//平面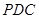 ;
;
(2)求证: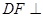 平面
平面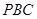 ;
;
(3)求点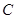 到平面
到平面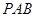 的距离。
的距离。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四棱柱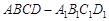 中,侧棱
中,侧棱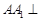 底面
底面 ,
,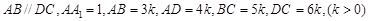
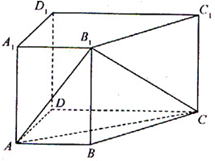
(Ⅰ)求证: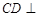 平面
平面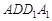
(Ⅱ)若直线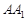 与平面
与平面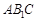 所成角的正弦值为
所成角的正弦值为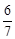 ,求
,求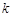 的值
的值
(Ⅲ)现将与四棱柱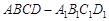 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为
形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为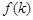 ,写出
,写出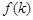 的解析式。(直接写出答案,不必说明理由)
的解析式。(直接写出答案,不必说明理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com