
经销商经销某种农产品,在一个销售季度内,每售出 t该产品获利润
t该产品获利润 元,未售出的产品,每
元,未售出的产品,每 t亏损
t亏损 元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示。经销商为下一个销售季度购进了
元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示。经销商为下一个销售季度购进了 t该农产品,以
t该农产品,以 (单位:t,
(单位:t, )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, (单位:元)表示下一个销售季度内销商该农产品的利润。
(单位:元)表示下一个销售季度内销商该农产品的利润。

(1)将 表示为
表示为 的函数;
的函数;
(2)根据直方图估计利润 不少于57000元的概率;
不少于57000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若 ,则取
,则取 ,且
,且 的概率等于需求量落入
的概率等于需求量落入 的概率),求利润
的概率),求利润 的数学期望.
的数学期望.
(1) 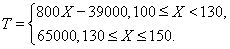 ;(2) 0.7.
;(2) 0.7.
(3)T的分布列为:
T | 45 000 | 53 000 | 61 000 | 65 000 |
P | 0.1 | 0.2 | 0.3 | 0.4 |
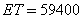 .
.
【解析】
试题分析:(1)当X<130时,会有一部分损失,而X>130,故以130为界分两种情况分别求出利润T与X的关系式.(2)利用(1)所得解析式及利润T不少于57 000元,解不等式即可得X的范围.再根据频率分布直方图便可得下一个销售季度内的利润T不少于57 000元的概率的估计值.(3)据题意,X取105、115、125、135、145这5个值,再根据直方图得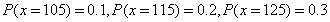 ,
,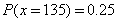 ,
,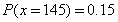 ,再利用(1)题所得函数式可得相应的利润及其对应的概率,从而得分布列及期望.
,再利用(1)题所得函数式可得相应的利润及其对应的概率,从而得分布列及期望.
试题解析:(1)当X∈[100,130)时,T=500X-300(130-X)=800X-39000,
当X∈[130,150]时,T=500×130=65 000.
所以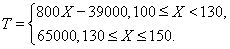
(2)由(1)知利润T不少于57 000元当且仅当120≤X≤150.
由直方图知需求量X∈[120,150]的频率为0.30+0.25+0.15=0.7,所以下一个销售季度内的利润T不少于57 000元的概率的估计值为0.7.
(3)依题意可得T的分布列为:
T | 45 000 | 53 000 | 61 000 | 65 000 |
P | 0.1 | 0.2 | 0.3 | 0.4 |
所以ET=45 000×0.1+53 000×0.2+61 000×0.3+65 000×0.4=59400.
考点:1、函数的应用;2、频率分布直方图及概率;3、随机变量的分布列及期望.


科目:高中数学 来源: 题型:
 经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川成都外国语学校高三下二月月考文科数学试卷(解析版) 题型:解答题
经销商经销某种农产品,在一个销售季度内,每售出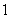 t该产品获利润
t该产品获利润 元,未售出的产品,每
元,未售出的产品,每 t亏损
t亏损 元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示。经销商为下一个销售季度购进了
元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示。经销商为下一个销售季度购进了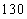 t该农产品,以
t该农产品,以 (单位:t,
(单位:t, )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, (单位:元)表示下一个销售季度内销商该农产品的利润。
(单位:元)表示下一个销售季度内销商该农产品的利润。

(1)将 表示为
表示为 的函数;(2)根据直方图估计利润
的函数;(2)根据直方图估计利润 不少于57000元的概率.
不少于57000元的概率.
查看答案和解析>>
科目:高中数学 来源:2013年全国普通高等学校招生统一考试文科数学(新课标2卷解析版) 题型:解答题
经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如右图所示.经销商为下一个销售季度购进了130t该农产品.以 (单位:t,100≤
(单位:t,100≤ ≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.

(Ⅰ)将T表示为 的函数;
的函数;
(Ⅱ)根据直方图估计利润T不少于57000元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com