【题目】我市某机构调查小学生课业负担的情况，设平均每人每天做作业时间为X(单位：分钟)，按时间分下列四种情况统计：①0～30分钟；②30～60分钟；③60～90分钟；④90分钟以上，有1000名小学生参加了此项调查，如图是此次调查中某一项的程序框图，其输出的结果是600，则平均每天做作业时间在0～60分钟内的学生的频率是（ ）
A. 0.20B. 0.80C. 0.60D. 0.40
一线名师提优试卷系列答案科目：高中数学 来源： 题型：
【题目】如图,正三棱柱ABC-A1B1C1中，D是AC中点，且直线AB1与平面BCC1B1所成的角为300，则异面直线AB1与BD所成角的大小为 （ ）
A. 300
B. 450
C. 600
D. 900
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知向量 
=（ 
sin 
，1）， 
=（cos ，cos2 ）． （Ⅰ）若 =1，求cos（ 
﹣x）的值；
（Ⅱ）记f（x）= ，在△ABC中，A、B、C的对边分别为a、b、c，且满足（2a﹣c）cosB=bcosC，求函数f（A）的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地区2011年至2017年农村居民家庭人均纯收入y(单位：千元)的数据如下表：
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求样本中心点坐标；
(2)已知两变量线性相关，求y关于t的线性回归方程；
(3)利用(2)中的线性回归方程，分析2011年至2017年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2019年农村居民家庭人均纯收入.
附：回归直线的斜率和截距的最小二乘估计公式分别为：
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一只药用昆虫的产卵数
与一定范围内的温度
有关，现收集了该种药用昆虫的6组观测数据如下表：
温度 | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数 | 6 | 11 | 20 | 27 | 57 | 77 |
（1）若用线性回归模型，求关于的回归方程
（精确到0.1）；
（2）若用非线性回归模型求关的回归方程为
，且相关指数
①试与（1）中的线性回归模型相比，用
说明哪种模型的拟合效果更好.
②用拟合效果好的模型预测温度为
时该种药用昆虫的产卵数（结果取整数）.
附：一组数据
，其回归直线的斜率和截距的最小二乘估计为
；相关指数
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知不等式|x+3|＜2x+1的解集为{x|x＞m}． （Ⅰ）求m的值；
（Ⅱ）设关于x的方程|x﹣t|+|x+ 
|=m（t≠0）有解，求实数t的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
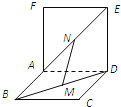
【题目】如图，两个正方形ABCD和ADEF所在平面互相垂直，设M、N分别是BD和AE的中点，那么
；
面CDE；
；
MN,CE异面其中正确结论的序号是______．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
