
设数列 的首项
的首项 ,前n项和为Sn ,且满足
,前n项和为Sn ,且满足 ( n∈N*) .则满足
( n∈N*) .则满足 的所有n的和为 .
的所有n的和为 .
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:填空题
已知无穷数列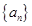 具有如下性质:①
具有如下性质:① 为正整数;②对于任意的正整数
为正整数;②对于任意的正整数 ,当
,当 为偶数时,
为偶数时, ;当
;当 为奇数时,
为奇数时, .在数列
.在数列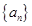 中,若当
中,若当 时,
时, ,当
,当 时,
时, (
( ,
, ),则首项
),则首项 可取数值的个数为 (用
可取数值的个数为 (用 表示)
表示)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数,按照点或小石子能排列的形状对数进行分类,如图4中的实心点个数1,5,12,22,…, 被称为五角形数,其中第1个五角形数记作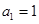 ,第2个五角形数记作
,第2个五角形数记作 ,第3个五角形数记作
,第3个五角形数记作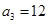 ,第4个五角形数记作
,第4个五角形数记作 ,……,若按此规律继续下去,若
,……,若按此规律继续下去,若 ,则
,则 .
.
1 5 12 22
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com