
【题目】若f(x)=x3+ax2+bx+c有两个极值点x1 , x2且f(x1)=x1 , 则关于x的方程3[(f(x)]2+2af(x)+b=0的不同实根个数为( )
A.2
B.3
C.4
D.不确定
【答案】B
【解析】解:∵函数f(x)=x3+ax2+bx+c有两个极值点x1 , x2 , 不妨设x1<x2 , ∴f′(x)=3x2+2ax+b=0有两个不相等的实数根,
∴△=4a2﹣12b>0.解得x= ![]() .
.
∵x1<x2 ,
∴x1= ![]() ,x2=
,x2= ![]() .
.
而方程3(f(x))2+2af(x)+b=0的△1=△>0,
∴此方程有两解且f(x)=x1或x2 .
不妨取0<x1<x2 , f(x1)>0.
①把y=f(x)向下平移x1个单位即可得到y=f(x)﹣x1的图象,
∵f(x1)=x1 , 可知方程f(x)=x1有两解.
②把y=f(x)向下平移x2个单位即可得到y=f(x)﹣x2的图象,
∵f(x1)=x1 , ∴f(x1)﹣x2<0,可知方程f(x)=x2只有一解.
综上①②可知:方程f(x)=x1或f(x)=x2 . 只有3个实数解.
即关于x的方程3(f(x))2+2af(x)+b=0的只有3不同实根.
故选:B.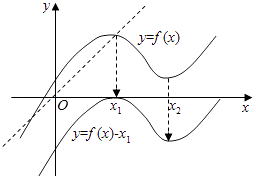
【考点精析】通过灵活运用函数的极值与导数,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值即可以解答此题.
是极小值即可以解答此题.


科目:高中数学 来源: 题型:
【题目】设a≥0,f(x)=x﹣1﹣ln2x+2alnx(x>0). (Ⅰ)令F(x)=xf′(x),讨论F(x)在(0,+∞)内的单调性并求极值;
(Ⅱ)求证:当x>1时,恒有x>ln2x﹣2alnx+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx﹣a+2
(1)若关于x的不等式f(x)>0的解集是(﹣1,3),求实数a,b的值;
(2)若b=2,a>0,解关于x的不等式f(x)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对某渔业产品的质量调研中,从甲、乙两地出产的该产品中各随机抽取10件,测量该产品中某种元素的含量(单位:毫克).如图是测量数据的茎叶图: 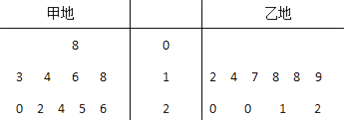
规定:当产品中的此种元素含量≥15毫克时为优质品.
(Ⅰ)试用上述样本数据估计甲、乙两地该产品的优质品率(优质品件数/总件数);
(Ⅱ)从乙地抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优质品数ξ的分布列及数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在△ABC中,D、F分别是BC、AC的中点, ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() .
. 
(1)用 ![]() 、
、 ![]() 表示向量
表示向量 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() ;
;
(2)求证:B、E、F三点共线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com