
��1������ԲC�ϵĵ�A��1,![]() ����F1��F2����ľ���֮�͵���4��д����ԲC�ķ��̺ͽ�������.
����F1��F2����ľ���֮�͵���4��д����ԲC�ķ��̺ͽ�������.
��2�����K�ǣ�1����������Բ�ϵĶ��㣬���߶�F1K���е�Ĺ켣����.
��3����֪��Բ�������ʣ���M��N����ԲC�Ϲ���ԭ��ԳƵ������㣬��P����Բ������һ�㣬��ֱ��PM��PN��б�ʶ����ڣ�����ΪkPM��kPNʱ����ôkPM��kPN֮�������Pλ���صĶ�ֵ����д��˫����![]() =1�����������Ե����ʲ�����֤��.
=1�����������Ե����ʲ�����֤��.
����:����֪������д����Բ���̼����뷨��켣�����ⲻ��ֱ��֤����Բ�е����ʣ��������Ƶ�ת����˫������֤��˫���߾��е�����,��б�ʹ�ʽ��˫���߷��̼��ɵ�֤.
��:��1����ԲC�Ľ�����x���ϣ�����Բ�ϵĵ�A��F1��F2����ľ���֮����4����2a=4����a=2.
�ֵ�A��1��![]() ������Բ�ϣ����
������Բ�ϣ����![]() +
+![]() =1,b2=3.
=1,b2=3.
��c2=a2-b2=1.
����ԲC�ķ���Ϊ![]() +
+![]() =1,����F1��-1��0����F2��1��0��.
=1,����F1��-1��0����F2��1��0��.
(2)����ԲC�ϵĶ���ΪK(x1,y1)���߶�F1K���е�Q��x,y������x=![]() ,y=
,y=![]() ,
,
��x1=2x+1,y1=2y.
��![]() +
+![]() =1,����x+
=1,����x+![]() ��2+
��2+![]() =1Ϊ����Ĺ켣����.
=1Ϊ����Ĺ켣����.
��3�����Ƶ�����Ϊ����M��N��˫����![]() =1�Ϲ���ԭ��ԳƵ������㣬��P��˫����������һ�㣬��ֱ��PM��PN��б�ʶ����ڣ�����ΪkPM��kPNʱ����ôkPM��kPN֮�������Pλ���صĶ�ֵ.���M������Ϊ��m,n�������N������Ϊ��-m,-n��������
=1�Ϲ���ԭ��ԳƵ������㣬��P��˫����������һ�㣬��ֱ��PM��PN��б�ʶ����ڣ�����ΪkPM��kPNʱ����ôkPM��kPN֮�������Pλ���صĶ�ֵ.���M������Ϊ��m,n�������N������Ϊ��-m,-n��������![]() =1.
=1.
�����P��������x,y������kPM=![]() ,
,
kPN=![]() ,��kPM��kPN=
,��kPM��kPN=![]() ��
��![]() =
=![]() .
.
��y2=![]() x2-b2,n2=
x2-b2,n2=![]() m2-b2,�����kPM��kPN=
m2-b2,�����kPM��kPN=![]() .
.
��ɫͨ��
��ȶ������������ѧ��ѧ��������һ�����⣬���ܺܺõ�����ѧ��̽�������������Ӧ�ø����㹻������.����Ȥ��ͬѧҲ��֤����Բ���е�����.������о�Բ���ߵ�һ�ַ���.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��a��b��0���������������㣬��ԲC�ϵĵ�
��a��b��0���������������㣬��ԲC�ϵĵ�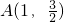 ������ľ���֮�͵���4��
������ľ���֮�͵���4�� ��|PQ|�����ֵ��
��|PQ|�����ֵ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com