
【题目】某公司为了解用户对其产品的满意度,从A、B两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
A地区: | 62 | 73 | 81 | 92 | 95 | 85 | 74 | 64 | 53 | 76 |
78 | 86 | 95 | 66 | 97 | 78 | 88 | 82 | 76 | 89 | |
B地区: | 73 | 83 | 62 | 51 | 91 | 46 | 53 | 73 | 64 | 82 |
93 | 48 | 95 | 81 | 74 | 56 | 54 | 76 | 65 | 79 |
(Ⅰ)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度的平均值及分散程度(不要求算出具体值,给出结论即可):
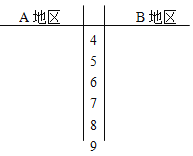
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
记事件C:“A地区用户的满意度等级高于B地区用户的满意度等级”,假设两地区用户的评价结果相互独立,根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率。
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,
, ![]() (
(![]() 在
在![]() 轴上方),且
轴上方),且![]() .设点
.设点![]() 在
在![]() 轴上的射影为
轴上的射影为![]() ,三角形
,三角形![]() 的面积为2(如图1).
的面积为2(如图1).
(1)求椭圆的方程;
(2)设平行于![]() 的直线与椭圆相交,其弦的中点为
的直线与椭圆相交,其弦的中点为![]() .
.
①求证:直线![]() 的斜率为定值;
的斜率为定值;
②设直线![]() 与椭圆相交于两点
与椭圆相交于两点![]() ,
, ![]() (
(![]() 在
在![]() 轴上方),点
轴上方),点![]() 为椭圆上异于
为椭圆上异于![]() ,
, ![]() ,
, ![]() ,
, ![]() 一点,直线
一点,直线![]() 交
交![]() 于点
于点![]() ,
, ![]() 交
交![]() 于点
于点![]() ,如图2,求证:
,如图2,求证: ![]() 为定值.
为定值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 是圆心为
是圆心为![]() ,半径为1的圆.
,半径为1的圆.
(1)求曲线![]() ,
, ![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上的点,
上的点, ![]() 为曲线
为曲线![]() 上的点,求
上的点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,…,第五组,如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )

A. 6 B. 8
C. 12 D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点坐标为
的一个焦点坐标为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,过点
,过点![]() 的直线
的直线![]() (与
(与![]() 轴不重合)与椭圆
轴不重合)与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,试证明:直线
,试证明:直线![]() 与
与![]() 轴平行.
轴平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018贵州遵义市高三上学期第二次联考】设抛物线![]() 的准线与
的准线与![]() 轴交于
轴交于![]() ,抛物线的焦点为
,抛物线的焦点为![]() ,以
,以![]() 为焦点,离心率
为焦点,离心率![]() 的椭圆与抛物线的一个交点为
的椭圆与抛物线的一个交点为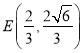 ;自
;自![]() 引直线交抛物线于
引直线交抛物线于![]() 两个不同的点,设
两个不同的点,设![]() .
.
(Ⅰ)求抛物线的方程和椭圆的方程;
(Ⅱ)若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】衡阳市为增强市民的环境保护意识,面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名后按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,则应从第3,4,5组各抽取多少名志愿者?
(2)在(1)的条件下,该市决定在第3,4组的志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com