
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() ,
,![]() 为
为![]() 的中点.
的中点.
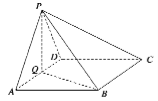
(1)若![]() ,求证:
,求证:![]() ;
;
(2)若![]() ,且
,且![]() ,点
,点![]() 在线段
在线段![]() 上,试确定点
上,试确定点![]() 的位置,使二面角
的位置,使二面角![]() 大小为
大小为![]() ,并求出
,并求出![]() 的值.
的值.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】某车间甲组有10名工人,其中有4名女工人;乙组有10名工人,其中有6名女工人.现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组共抽取4名工人进行技术考核.
(1)求从甲、乙两组各抽取的人数;
(2)求从甲组抽取的工人中恰有1名女工人的概率;
(3)求抽取的4名工人中恰有2名男工人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是坐标原点,若椭圆
是坐标原点,若椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,
,![]() 为椭圆
为椭圆![]() 上两动点,若有
上两动点,若有![]() ,证明:直线
,证明:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十一国庆节期间,某商场举行购物抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为![]() ,中奖可以获得3分;方案乙的中奖率为
,中奖可以获得3分;方案乙的中奖率为![]() ,中奖可以获得2分;未中奖则不得分,每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,抽奖结束后凭分数兑换奖品.
,中奖可以获得2分;未中奖则不得分,每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,抽奖结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为![]() ,求
,求![]() 的概率;
的概率;
(2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,分别求两种方案下小明、小红累计得分的分布列,并指出为了累计得分较大,两种方案下他们选择何种方案较好,并给出理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)令![]() ,是否存在实数
,是否存在实数![]() ,当
,当![]() (
(![]() 是自然常数)时,函数
是自然常数)时,函数![]() 的最小值是3,若存在,求出
的最小值是3,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(3)当![]() 时,证明:
时,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)若函数![]() 在
在![]() 处有极值,求函数
处有极值,求函数![]() 的最大值;
的最大值;
(2)①是否存在实数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立?若存在,求出
上恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
②证明:不等式![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com