已知椭圆的两个焦点分别为
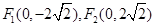
,离心率
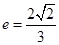
.
(1)求椭圆的方程.
(2)一条不与坐标轴平行的直线
与椭圆交于不同的两点
,且线段
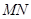
的中点的横坐标为
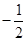
,求直线
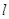
的斜率的取值范围.
(1)设椭圆方程为
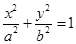
,由已知
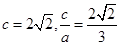
,
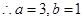
椭圆方程为

。——————5分
(2)设
方程为
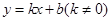
,联立
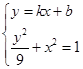
得
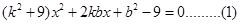
————————7分
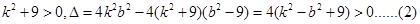

————————9分
由(3)的
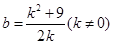
代入(2)的
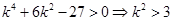
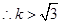
或
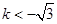
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:单选题
过点
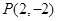
且与
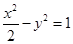
有相同渐近线的双曲线方程是
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
连接椭圆
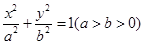
的一个焦点和一个顶点得到的直线方程为
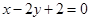
,则该椭圆的离心率为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分).
如图,已知某椭圆的焦点是
F1(-4,0)、
F2(4,0),过点
F2并垂直于
x轴的直线与椭圆的一个交点为
B,且|
F1B|+|
F2B|=10,椭圆上不同的两点
A(
x1,
y1),
C(
x2,
y2)满足条件:|
F2A|、|
F2B|、|
F2C|成等差数列.
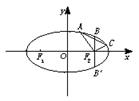
(1)求该弦椭圆的方程;
(2)求弦
AC中点的横坐标;
(3)设弦
AC的垂直平分线的方程为
y=
kx+
m,求
m的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
若椭圆
C1:
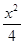
+
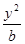
=1(0<
b<2)的离心率等于
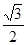
,抛物线
C2:
x2=2
py(
p>0)的焦点在椭圆
C1的顶点上.
(Ⅰ)求抛物线
C2的方程;
(Ⅱ)若过
M(-1,0)的直线
l与抛物线
C2交于
E、
F两点,又过
E、
F作抛物线
C2的切线
l1、
l2,当
l1⊥
l2时,求直线
l的方程.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
与椭圆
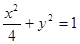
有相同的焦点且过点P
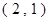
的双曲线方程是
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
点
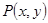
是椭圆
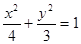
上的动点,
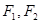
为其左、右焦点,则
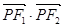
的取值范围是
▲
。
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
椭圆
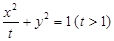
上一焦点与短轴两端点形成的三角形的面积为1,则

.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(18分)已知椭圆C:
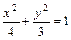
,在曲线C上是否存在不同两点A、B关于直线
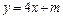
(m为常数)对称?若存在,求出
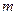
满足的条件;若不存在,说明理由。
查看答案和解析>>

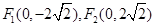 ,离心率
,离心率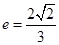 .
.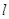 与椭圆交于不同的两点
与椭圆交于不同的两点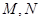 ,且线段
,且线段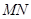 的中点的横坐标为
的中点的横坐标为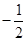 ,求直线
,求直线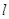 的斜率的取值范围.
的斜率的取值范围.
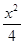 +
+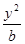 =1(0<b<2)的离心率等于
=1(0<b<2)的离心率等于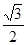 ,抛物线C2:x2=2py(p>0)的焦点在椭圆C1的顶点上.
,抛物线C2:x2=2py(p>0)的焦点在椭圆C1的顶点上.