练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知数列的前项和为，满足且，数列的前项为，满足

    （Ⅰ）设，求证：数列为等比数列；

    （Ⅱ）求的通项公式；

    （Ⅲ）若对任意的恒成立，求实数的最大值.

    【答案】（Ⅰ）见解析（Ⅱ）（Ⅲ）

    【解析】

    （Ⅰ）对递推公式变形可得，根据等比数列的定义，即可得证；

    （Ⅱ）化简可得，然后再利用裂项相消法求和，即可得到结果；

    （Ⅲ）先求出，然后再利用分组求和求出，然后再利用分离常数法，可得，最后对进行分类讨论，即可求出结果．

    解：（Ⅰ）由得，变形为：，

    ，且

    ∴数列是以首项为2，公比为的等比数列

    （Ⅱ）由

    ；

    （Ⅲ）由（Ⅰ）知数列是以首项为2，公比为的等比数列

    ∴，于是

    ∴=，由得

    从而 ， ∴

    当n为偶数时，恒成立，而，∴1

    当n为奇数时，恒成立，而，∴

    综上所述，，即的最大值为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设正数、满足会且使得关于的不等式总有实数解.试求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数为常数．

    （Ⅰ）若是函数的一个极值点，求此时函数的单调区间；

    （Ⅱ）若对任意的，，不等式恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有12支球队进行足球比赛,每两队都赛一场,胜者得3分,负者得0分,平局各得1分那么,有1支球队最少要得多少分才能保证最多有6支球队的得分不少于该队的得分?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是一个长方体，从点到直线、、的垂线分别交直线、、于点、、，垂足分别为、、．求证：

    （1）、、三点共线；

    （2）、、三条直线交于一点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为坐标原点，椭圆的焦距为，直线截圆与椭圆所得的弦长之比为，圆、椭圆与轴正半轴的交点分别为，.

    （1）求椭圆的标准方程；

    （2）设点（且）为椭圆上一点，点关于轴的对称点为，直线，分别交轴于点，，证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四边形中，，，，．

    （1）求的长；

    （2）若，求四边形的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市每年春节前后,由于大量的烟花炮竹的燃放,空气污染较为严重．该市环保研究所对近年春节前后每天的空气污染情况调查研究后发现,每天空气污染的指数．f（t），随时刻t（时）变化的规律满足表达式，其中a为空气治理调节参数,且a∈（0，1）．

    (1)令,求x的取值范围；

    (2)若规定每天中f（t）的最大值作为当天的空气污染指数,要使该市每天的空气污染指数不超过5,试求调节参数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

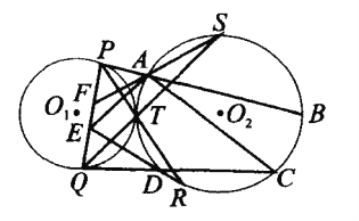
    【题目】如图，两圆外切于点T， PQ为的弦，直线PT、QT分别交于点R、S，分别过P、Q作的切线依次交于A、B、D、C，直线RD、SA分别交PQ于E、F。求证：。

    查看答案和解析>>

    同步练习册答案