
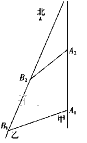
【题目】如图,甲船以每小时30![]() 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10![]() 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
【答案】30![]()
【解析】试题分析:解法一:连接![]() ,依题意可得
,依题意可得![]() ,求得
,求得![]() 的值,推断出
的值,推断出![]() 是等比三角形,进而求得
是等比三角形,进而求得![]() ,在
,在![]() 中,利用余弦定理求得
中,利用余弦定理求得![]() 的值,进而求得乙船的速度
的值,进而求得乙船的速度
解法二:连接![]() ,先计算出
,先计算出![]() ,从而得到
,从而得到![]() ,由余弦定理计算出
,由余弦定理计算出![]() ,再计算出
,再计算出![]() ,得到
,得到![]() ,解三角形求出
,解三角形求出![]() 的值
的值
解析:解法一:如图,连结A1B2,
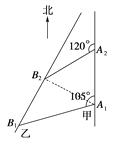
由题意知A2B2=10![]() n mile,A1A2=30
n mile,A1A2=30![]() ×
×![]() =10
=10![]() n mile.
n mile.
所以A1A2=A2B2.
又∠A1A2B2=180°-120°=60°,
所以△A1A2B2是等边三角形.
所以A1B2=A1A2=10![]() n mile.
n mile.
由题意知,A1B1=20 n mile,∠B1A1B2=105°-60°=45°,
在△A1B2B1中,由余弦定理,得B1B=A1B+A1B-2A1B1·A1B2·cos45°=202+(10![]() )2-2×20×10
)2-2×20×10![]() ×
×![]() =200.
=200.
所以B1B2=10![]() n mile.
n mile.
因此,乙船速度的大小为![]() ×60=30
×60=30![]() (n mile/h).
(n mile/h).
答:乙船每小时航行30![]() n mile.
n mile.
解法二:如下图所示,连结A2B1,
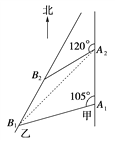
由题意知A1B1=20 n mile,A1A2=30![]() ×
×![]()
=10![]() n mile,∠B1A1A2=105°,
n mile,∠B1A1A2=105°,
又cos105°=cos(45°+60°)
=cos45°cos60°-sin45°sin60°=![]() ,
,
sin105°=sin(45°+60°)=sin45°cos60°+cos45°sin60°
=![]() ,
,
在△A2A1B1中,由余弦定理,得A2B=A1B+A1A-2A1B1·A1A2·cos105°=202+(10![]() )2-2×20×10
)2-2×20×10![]() ×
×![]() =100(4+2
=100(4+2![]() ),
),
所以A2B1=10(1+![]() )n mile
)n mile
由正弦定理,得sin∠A1A2B1=![]() ·sin∠B1A1A2=
·sin∠B1A1A2=![]() ×
×![]() =
=![]() ,
,
所以∠A1A2B1=45°,即∠B1A2B2=60°-45°=15°,cos15°=sin105°=![]() .
.
在△B1A2B2中,由题知A2B2=10![]() n mile,
n mile,
由余弦定理,得B1B=A2B+A2B-2A2B1·A2B2·cos15°=102(1+![]() )2+(10
)2+(10![]() )2-2×10(1+
)2-2×10(1+![]() )×10
)×10![]() ×
×![]() =200,
=200,
所以B1B2=10![]() n mile,故乙船速度的大小为
n mile,故乙船速度的大小为![]() ×60=30
×60=30![]() (n mile/h).
(n mile/h).
答:乙船每小时航行30![]() n mile.
n mile.


科目:高中数学 来源: 题型:
【题目】一批产品中,有一级品100个,二级品60个,三级品40个,分别用系统抽样和分层抽样的方法,从这批产品中抽取一个容量为20的样本,写出抽样过程,并说明采用哪种抽样方法更能反映总体水平.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.

根据该折线图,下列结论错误的是( )
A. 月接待游客量逐月增加
B. 年接待游客量逐年增加
C. 各年的月接待游客量高峰期大致在7,8月
D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() ,
,![]() ,
,![]() 具有性质
具有性质![]() ;对任意
;对任意![]() ,
,![]() ,
,![]() 与
与![]() 两数中至少有一个是该数列中的一项,给出下列三个结论:
两数中至少有一个是该数列中的一项,给出下列三个结论:
①数列![]() ,
,![]() ,
,![]() ,
,![]() 具有性质
具有性质![]() ;
;
②若数列![]() 具有性质
具有性质![]() ,则
,则![]() ;
;
③若数列![]() ,
,![]() ,
,![]() 具有性质
具有性质![]() ,则
,则![]() .
.
其中,正确结论的个数是( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的可导函数,且满足f′(x)>f(x),对任意的正数a,下面不等式恒成立的是( )
A.f(a)<eaf(0)
B.f(a)>eaf(0)
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x和所支出的维修费用y(单位:万元)有如下的统计资料:
使用年限x/年 | 2 | 3 | 4 | 5 | 6 |
维修费用y/万元 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知y对x呈线性相关关系.试求:
(1)回归方程![]() x+
x+![]() 的系数
的系数![]() .
.
(2)使用年限为10年时,试估计维修费用是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com