
ҰңМвДүҰүҢьЖЪӘ¬Ді№«Ң»№«ЛңУлТшРРүҒХ№ФЖЙБё¶іЛіµЦ§ё¶»о¶ҮӘ¬ОьТэБЛЦЪ¶аіЛүНК№УГХвЦЦЦ§ё¶·ҢКҢӘ®ДіПЯВ·№«Ң»іµЧә±ёУГ20МмК±әдүҒХ№НЖ№г»о¶ҮӘ¬ЛыГЗЧйЦҮУР№Ш№¤ЧчИЛФ±Ә¬¶Ф»о¶ҮµДЗ°ЖЯМмК№УГФЖЙБё¶Ц§ё¶µДИЛөОКэңЭЧцБЛіхІҢө¦АнӘ¬ЙиµЪxМмК№УГФЖЙБё¶Ц§ё¶µДИЛөООҒyӘ¬µГµҢИзНәЛщКңµДЙұµгНәӘ®
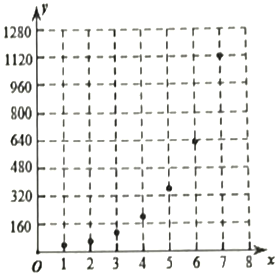
УЙНіәЖНә±нүЙЦҒӘ¬үЙУГғҮКэyӘҢabxДвғПyУлxµД№ШПµ
ӘЁ1Ә©Зуy№ШУЪxµД»Ш№й·ҢіМӘ»
ӘЁ2Ә©Ф¤ІвНЖ№гЖЪДЪµЪәёМмЖрК№УГФЖЙБё¶Ц§ё¶µДИЛөОҢ«і¬№э10000ИЛөОӘ®
ёҢӘғұЩІОүәКэңЭ
|
|
|
|
|
|
4 | 360 | 2.30 | 140 | 14710 | 71.40 |
±нЦРviӘҢlgyiӘ¬![]() lgyi
lgyi
ұЪІОүә№«КҢӘғ¶ФУЪТ»ЧйКэңЭӘЁu1Ә¬v1Ә©Ә¬ӘЁu2Ә¬v2Ә©ҰӘ¬ӘЁunӘ¬vnӘ©Ә¬Жд»Ш№йЦ±ПЯvӘҢ¦Б+¦ВuµДР±ВКғНҢШңаµДЧоРҰ¶юіЛ№АәЖ·Ц±рОҒ¦В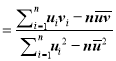 Ә¬¦Б
Ә¬¦Б![]() Ә®
Ә®
Ұңөр°ёҰүӘЁ1Ә©yӘҢ100.25x+1.3Ә»ӘЁ2Ә©Ф¤ІвНЖ№гЖЪДЪµЪ11МмЖрК№УГФЖЙБё¶Ц§ё¶µДИЛөОҢ«і¬№э10000ИЛөО
ҰңҢвОцҰү
ӘЁ1Ә©ПИ¶ФyӘҢabxБҢ±ЯН¬ИҰТФ10ОҒµЧµД¶ФКэӘ¬µГµҢvӘҢxlgb+lgaӘ¬ФЩёщңЭР±ВКғНҢШңаµДµДЧоРҰ¶юіЛ·Ё№АәЖµГµҢlgbғНlgaӘ¬өУ¶шµГµҢ![]() Ә¬ФЩРөіцy№ШУЪxµДПЯРФ»Ш№й·ҢіМӘ»ӘЁ2Ә©ёщңЭӘЁ1Ә©ЛщµГµДПЯРФ»Ш№й·ҢіМӘ¬µГµҢ100.25x+1.3Әң10000Ә¬Ңвіц
Ә¬ФЩРөіцy№ШУЪxµДПЯРФ»Ш№й·ҢіМӘ»ӘЁ2Ә©ёщңЭӘЁ1Ә©ЛщµГµДПЯРФ»Ш№й·ҢіМӘ¬µГµҢ100.25x+1.3Әң10000Ә¬Ңвіц![]() µД·¶О§Ә¬µГµҢөр°ё.
µД·¶О§Ә¬µГµҢөр°ё.
ӘЁ1Ә©УЙyӘҢabxӘ¬БҢ±ЯН¬К±ИҰТФ10ОҒµЧµД¶ФКэӘ¬
µГlgyӘҢlga+xlgbӘ¬әөvӘҢxlgb+lgaӘ¬
УЙЧоРҰ¶юіЛ·ЁµГӘғlgb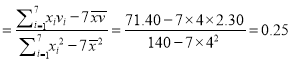 Ә®
Ә®
ҰЯvӘҢxlgb+lga№эµгӘЁ4Ә¬2.30Ә©Ә¬
ҰаlgaӘҢ2.30©Ѓ0.25ҰБ4ӘҢ1.3Ә®
ҰаaӘҢ101.3Ә¬bӘҢ100.25Ә®
Ұаy№ШУЪxµДПЯРФ»Ш№й·ҢіМОҒyӘҢ101.3100.25xӘҢ100.25x+1.3Ә»
ӘЁ2Ә©УЙ100.25x+1.3Әң10000Ә¬µГ0.25x+1.3Әң4Ә¬ҢвµГxӘң10.8Ә®
УЦҰЯxҰКN*Ә¬ҰаФ¤ІвНЖ№гЖЪДЪµЪ11МмЖрК№УГФЖЙБё¶Ц§ё¶µДИЛөОҢ«і¬№э10000ИЛөОӘ®


 МмМмПтЙПТ»±ңғГңнПµБРөр°ё
МмМмПтЙПТ»±ңғГңнПµБРөр°ё РҰС§Йъ10·ЦЦУУ¦УГМвПµБРөр°ё
РҰС§Йъ10·ЦЦУУ¦УГМвПµБРөр°ё
| Дкә¶ | ёЯЦРүОіМ | Дкә¶ | іхЦРүОіМ |
| ёЯТ» | ёЯТ»Гв·СүОіМНЖәцӘҰ | іхТ» | іхТ»Гв·СүОіМНЖәцӘҰ |
| ёЯ¶ю | ёЯ¶юГв·СүОіМНЖәцӘҰ | іх¶ю | іх¶юГв·СүОіМНЖәцӘҰ |
| ёЯИэ | ёЯИэГв·СүОіМНЖәцӘҰ | іхИэ | іхИэГв·СүОіМНЖәцӘҰ |
үЖДүӘғёЯЦРКэС§ АөФөӘғ МвРНӘғ
ҰңМвДүҰүТСЦҒғҮКэ![]()
ӘЁ1Ә©ЗуЦ¤Әғ![]()
ӘЁ2Ә©ИфғҮКэ![]() µДНәПуУлЦ±ПЯ
µДНәПуУлЦ±ПЯ![]() Г»УРҢ»µгӘ¬ЗуКµКэ
Г»УРҢ»µгӘ¬ЗуКµКэ![]() µДИҰЦµ·¶О§Ә»
µДИҰЦµ·¶О§Ә»
ӘЁ3Ә©ИфғҮКэ![]() Ә¬ФтКЗ·сөжФЪКµКэ
Ә¬ФтКЗ·сөжФЪКµКэ![]() Ә¬К№µГ
Ә¬К№µГ![]() µДЧоРҰЦµОҒ
µДЧоРҰЦµОҒ![]() ӘүИфөжФЪӘ¬Зуіц
ӘүИфөжФЪӘ¬Зуіц![]() µДЦµӘ»ИфІ»өжФЪӘ¬ЗлЛµГчАнУЙӘ®
µДЦµӘ»ИфІ»өжФЪӘ¬ЗлЛµГчАнУЙӘ®
Ійүөөр°ёғНҢвОц>>
үЖДүӘғёЯЦРКэС§ АөФөӘғ МвРНӘғ
ҰңМвДүҰүФЪЦ±ҢЗЧш±кПµxOyЦРӘ¬әЗғҮКэ![]() µДНәПуОҒЗъПЯC1Ә¬ғҮКэ
µДНәПуОҒЗъПЯC1Ә¬ғҮКэ![]() µДНәПуОҒЗъПЯC2Ә®
µДНәПуОҒЗъПЯC2Ә®
ӘЁұсӘ©±ИҢПfӘЁ2Ә©ғН1µДөуРҰӘ¬ІұЛµГчАнУЙӘ»
ӘЁұтӘ©µ±ЗъПЯC1ФЪЦ±ПЯyӘҢ1µДПВ·ҢК±Ә¬ЗуxµДИҰЦµ·¶О§Ә»
ӘЁұуӘ©Ц¤ГчӘғЗъПЯC1ғНC2Г»УРҢ»µгӘ®
Ійүөөр°ёғНҢвОц>>
үЖДүӘғёЯЦРКэС§ АөФөӘғ МвРНӘғ
ҰңМвДүҰүДіФЛК乫ЛңҢУКЬБЛПтү№ғйңИФЦµШЗшГүМмЛНЦБЙЩ![]() Ц§Ф®ОпЧКµДИООсӘ®ёГ№«ЛңУР
Ц§Ф®ОпЧКµДИООсӘ®ёГ№«ЛңУР![]() БңФШЦШ
БңФШЦШ![]() µД
µД![]() РНүЁіµУл
РНүЁіµУл![]() БңФШЦШОҒ
БңФШЦШОҒ![]() µД
µД![]() РНүЁіµӘ¬УР
РНүЁіµӘ¬УР![]() ГыәЭК»Ф±Ә¬ГүБңүЁіµГүМмНщ·µµДөОКэОҒ
ГыәЭК»Ф±Ә¬ГүБңүЁіµГүМмНщ·µµДөОКэОҒ![]() РНүЁіµ
РНүЁіµ![]() өОӘ¬
өОӘ¬![]() РНүЁіµ
РНүЁіµ![]() өОӘ»ГүБңүЁіµГүМмНщ·µµДіЙ±ң·С
өОӘ»ГүБңүЁіµГүМмНщ·µµДіЙ±ң·С![]() РНОҒ
РНОҒ![]() ФҒӘ¬
ФҒӘ¬![]() РНОҒ
РНОҒ![]() ФҒӘ®ЗлОҒ№«Лң°ІЕЕТ»ПВӘ¬У¦ИзғОµчЕдіµБңӘ¬ІЕДЬК№№«ЛңЛщ»ЁµДіЙ±ң·СЧоµНӘүИфЦ»°ІЕЕ
ФҒӘ®ЗлОҒ№«Лң°ІЕЕТ»ПВӘ¬У¦ИзғОµчЕдіµБңӘ¬ІЕДЬК№№«ЛңЛщ»ЁµДіЙ±ң·СЧоµНӘүИфЦ»°ІЕЕ![]() РН»т
РН»т![]() РНүЁіµӘ¬Лщ»ЁµДіЙ±ң·С·Ц±рКЗ¶аЙЩӘү
РНүЁіµӘ¬Лщ»ЁµДіЙ±ң·С·Ц±рКЗ¶аЙЩӘү
Ійүөөр°ёғНҢвОц>>
үЖДүӘғёЯЦРКэС§ АөФөӘғ МвРНӘғ
ҰңМвДүҰүИзНәӘ¬ЛДАвЧ¶![]() µДµЧГжКЗХэ·ҢРОӘ¬
µДµЧГжКЗХэ·ҢРОӘ¬ ![]() Ә¬µгEФЪАвPBЙП.
Ә¬µгEФЪАвPBЙП.
ӘЁұсӘ©ЗуЦ¤ӘғЖҢГж![]() Ә»
Ә»
ӘЁұтӘ©µ±![]() ЗТEОҒPBµДЦРµгК±Ә¬ЗуAEУлЖҢГжPDBЛщіЙµДҢЗµДөуРҰ.
ЗТEОҒPBµДЦРµгК±Ә¬ЗуAEУлЖҢГжPDBЛщіЙµДҢЗµДөуРҰ.

Ійүөөр°ёғНҢвОц>>
үЖДүӘғёЯЦРКэС§ АөФөӘғ МвРНӘғ
ҰңМвДүҰүСҰРЮ4-4ӘғЧш±кПµУлІОКэ·ҢіМ
ФЪә«Чш±кПµЦРӘ¬Ц±ПЯ![]() µДә«Чш±к·ҢіМОҒ
µДә«Чш±к·ҢіМОҒ![]() Ә¬ПЦТФә«µг
Ә¬ПЦТФә«µг![]() ОҒФµгӘ¬ә«ЦбОҒ
ОҒФµгӘ¬ә«ЦбОҒ![]() ЦбµД·Зёғ°лЦбҢЁБұЖҢГжЦ±ҢЗЧш±кПµӘ¬ЗъПЯ
ЦбµД·Зёғ°лЦбҢЁБұЖҢГжЦ±ҢЗЧш±кПµӘ¬ЗъПЯ![]() µДІОКэ·ҢіМОҒ
µДІОКэ·ҢіМОҒ![]() ӘЁ
ӘЁ![]() ОҒІОКэӘ©.
ОҒІОКэӘ©.
ӘЁ1Ә©ЗуЦ±ПЯ![]() µДЦ±ҢЗЧш±к·ҢіМғНЗъПЯ
µДЦ±ҢЗЧш±к·ҢіМғНЗъПЯ![]() µДЖХНЁ·ҢіМӘ»
µДЖХНЁ·ҢіМӘ»
ӘЁ2Ә©ИфЗъПЯ![]() ОҒЗъПЯ
ОҒЗъПЯ![]() №ШУЪЦ±ПЯ
№ШУЪЦ±ПЯ![]() µД¶ФіЖЗъПЯӘ¬µг
µД¶ФіЖЗъПЯӘ¬µг![]() Ә¬
Ә¬![]() ·Ц±рОҒЗъПЯ
·Ц±рОҒЗъПЯ![]() ҰұЗъПЯ
ҰұЗъПЯ![]() ЙПµД¶ҮµгӘ¬µг
ЙПµД¶ҮµгӘ¬µг![]() Чш±кОҒ
Чш±кОҒ![]() Ә¬Зу
Ә¬Зу![]() µДЧоРҰЦµ.
µДЧоРҰЦµ.
Ійүөөр°ёғНҢвОц>>
үЖДүӘғёЯЦРКэС§ АөФөӘғ МвРНӘғ
ҰңМвДүҰүФЪЦ±ҢЗЧш±кПµ![]() ЦРӘ¬ЗъПЯCµДІОКэ·ҢіМОҒ
ЦРӘ¬ЗъПЯCµДІОКэ·ҢіМОҒ ОҒІОКэӘ®ФЪТФФµг
ОҒІОКэӘ®ФЪТФФµг![]() ОҒә«µгӘ¬ОҒІОКэӘ©Ә®ФЪТФФµг
ОҒә«µгӘ¬ОҒІОКэӘ©Ә®ФЪТФФµг![]() ОҒә«µгӘ¬ЦбµДХэ°лЦбОҒә«ЦбµДә«Чш±кПµЦРӘ¬Ц±ПЯ
ОҒә«µгӘ¬ЦбµДХэ°лЦбОҒә«ЦбµДә«Чш±кПµЦРӘ¬Ц±ПЯ![]() µДә«Чш±к·ҢіМОҒ
µДә«Чш±к·ҢіМОҒ![]() Ә®
Ә®
ӘЁұсӘ©ЗуЗъПЯCµДЖХНЁ·ҢіМғНЦ±ПЯ![]() µДЦ±ҢЗЧш±к·ҢіМӘ»
µДЦ±ҢЗЧш±к·ҢіМӘ»
ӘЁұтӘ©Йи![]() Ә¬Ц±ПЯ
Ә¬Ц±ПЯ![]() УлЗъПЯCҢ»УЪMӘ¬NБҢµгӘ¬Зу
УлЗъПЯCҢ»УЪMӘ¬NБҢµгӘ¬Зу![]() µДЦµӘ®
µДЦµӘ®
Ійүөөр°ёғНҢвОц>>
үЖДүӘғёЯЦРКэС§ АөФөӘғ МвРНӘғ
ҰңМвДүҰүЙи![]() Ұұ
Ұұ![]() Ұұ
Ұұ![]() ±нКңІ»Н¬µДЦ±ПЯӘ¬
±нКңІ»Н¬µДЦ±ПЯӘ¬![]() Ұұ
Ұұ![]() Ұұ
Ұұ![]() ±нКңІ»Н¬µДЖҢГжӘ¬ёшіцПВБР
±нКңІ»Н¬µДЖҢГжӘ¬ёшіцПВБР![]() ёцГьМвӘғЖдЦРГьМвХэИ·µДёцКэКЗӘЁ Ә©
ёцГьМвӘғЖдЦРГьМвХэИ·µДёцКэКЗӘЁ Ә©
ұЩИф![]() Ә¬ЗТ
Ә¬ЗТ![]() Ә¬Фт
Ә¬Фт![]() Ә»
Ә»
ұЪИф![]() Ә¬ЗТ
Ә¬ЗТ![]() Ә¬Фт
Ә¬Фт![]() Ә»
Ә»
ұЫИф![]() Ә¬
Ә¬![]() Ә¬
Ә¬![]() Ә¬Фт
Ә¬Фт![]() Ә»
Ә»
ұЬ Иф![]() Ә¬
Ә¬![]() Ә¬
Ә¬![]() Ә¬ЗТ
Ә¬ЗТ![]() Ә¬Фт
Ә¬Фт![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
Ійүөөр°ёғНҢвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
ғю±±КҰ»ӨБҒНшОӨ·ЁғНІ»БәРЕПұңЩ±ЁЖҢМЁ | НшЙПУРғ¦РЕПұңЩ±ЁЧЁЗш | µзРЕХ©ЖңЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРғ¦РЕПұңЩ±ЁЧЁЗш | ЙжЖуЗЦИЁңЩ±ЁЧЁЗш
ОӨ·ЁғНІ»БәРЕПұңЩ±Ёµз»°Әғ027-86699610 ңЩ±ЁУКПдӘғ58377363@163.com