
【题目】如图,A,B是半径为2的圆周上的定点,P为圆周上的动点,![]() 是锐角,大小为β.图中阴影区域的面积的最大值为
是锐角,大小为β.图中阴影区域的面积的最大值为
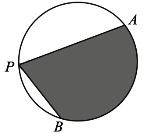
A. 4β+4cosβB. 4β+4sinβC. 2β+2cosβD. 2β+2sinβ
科目:高中数学 来源: 题型:
【题目】节能减排以来,兰州市100户居民的月平均用电量![]() 单位:度
单位:度![]() ,以
,以![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

![]() 求直方图中x的值;
求直方图中x的值;![]() 求月平均用电量的众数和中位数;
求月平均用电量的众数和中位数;
![]() 估计用电量落在
估计用电量落在![]() 中的概率是多少?
中的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个容量为66的样本,数据的分组及各组的频数如下:
[10.5,14.5) 2 [14.5,18.5) 4 [18.5,22.5) 9 [22.5,26.5) 18
[26.5,30.5) 11 [30.5,34.5) 12 [34.5,38.5) 8 [38.5,42.5) 2
根据样本的频率分布估计,数据落在[30.5,42.5)内的概率约是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司最近4年对某种产品投入的宣传费![]() 万元与年销售量
万元与年销售量![]() 之间的关系如下表所示.
之间的关系如下表所示.
| 1 | 4 | 9 | 16 |
| 168.6 | 236.6 | 304.6 | 372.6 |
(1)根据以上表格中的数据判断:![]() 与
与![]() 哪一个更适宜作为
哪一个更适宜作为![]() 与
与![]() 的函数模型?
的函数模型?
(2)已知这种产品的年利润![]() 万元与
万元与![]() 的关系为
的关系为![]() ,则年宣传费
,则年宣传费![]() 为多少时年利润最大?
为多少时年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各随机抽取了100件产品作为样本来检测一项质量指标值,若产品的该项质量指标值落在![]() 内,则为合格品,否则为不合格品.表1是甲套设备的样本的频数分布表,图是乙套设备的样本的频率分布直方图.
内,则为合格品,否则为不合格品.表1是甲套设备的样本的频数分布表,图是乙套设备的样本的频率分布直方图.

表甲套设备的样本的频数分布表
质量指标值 |
|
|
|
|
|
|
频数 | 2 | 10 | 36 | 38 | 12 | 2 |
(1)将频率视为概率.若乙套设备生产了10000件产品,则其中的合格品约有多少件?
(2)填写下面的2×2列联表,并判断能否在犯错误的概率不超过0.01的前提下,认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关.
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附表及公式: ,其中
,其中![]() ;
;
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2|x|.
(1)将函数f(x)写成分段函数;
(2)判断函数的奇偶性,并画出函数图象.
(3)若函数在[a, +∞)上单调,求a的范围。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com