
(本小题满分14分)已知定义域为 的函数
的函数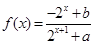 是奇函数
是奇函数
⑴求函数 的解析式;
的解析式;
⑵判断并证明函数 的单调性;
的单调性;
⑶若对于任意的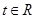 ,不等式
,不等式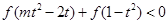 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(1)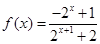 (2)减函数,证明见解析(3)
(2)减函数,证明见解析(3)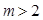
解析试题分析:⑴∵ 为奇函数,
为奇函数,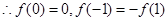
即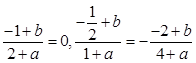 , 解得
, 解得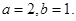
所以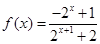 ,检验得
,检验得 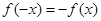 ,满足条件. …4分
,满足条件. …4分
⑵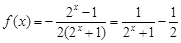 为
为 上的减函数
上的减函数
证明:设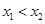
则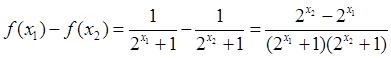
∵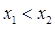
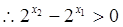 ,
, 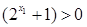
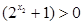

 即
即 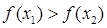

 为减函数 …8分
为减函数 …8分
⑶∵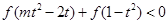 ,
, 
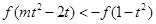
∵ 为奇函数,
为奇函数, ,
,
则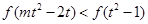 .
.
又 为减函数
为减函数 
 即
即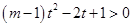 恒成立,
恒成立,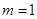 时显然不恒成立,
时显然不恒成立,
所以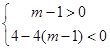
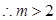 …14分
…14分
考点:本小题主要考查利用奇偶性求函数解析式,判断并证明函数的单调性,利用函数的单调性求解抽象不等式以及恒成立问题.
点评:如果奇函数在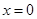 处有意义,则
处有意义,则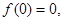 这一性质在解题时可以简化运算,特别好用,另外在用定义证明单调性时一定要把结果化到最简,尽量不要用已知函数的单调性来判断未知函数的单调性.解抽象不等式,关键是利用单调性“脱去”外层符号,得出具体的不等式,这一过程中要注意定义域是否有影响.
这一性质在解题时可以简化运算,特别好用,另外在用定义证明单调性时一定要把结果化到最简,尽量不要用已知函数的单调性来判断未知函数的单调性.解抽象不等式,关键是利用单调性“脱去”外层符号,得出具体的不等式,这一过程中要注意定义域是否有影响.


科目:高中数学 来源: 题型:解答题
(本小题15分)已知函数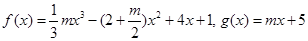 .
.
(1)当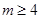 时,求
时,求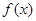 的单调递增区间;
的单调递增区间;
(2)是否存在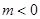 ,使得对任意的
,使得对任意的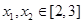 ,都有
,都有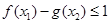 恒成立.若存在,求出
恒成立.若存在,求出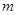 的取值范围; 若不存在,请说明理由.
的取值范围; 若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)星期天,刘先生到电信局打算上网开户,经询问,记录了可能需要的三种方式所花费的费用资料,现将资料整理如下:
1163普通:上网资费2元/小时;
2163A:每月50元(可上网50小时),超过50小时的部分资费2元/小时;
3ADSLD:每月70元,时长不限(其他因素忽略不计).
请你用所学的函数知识对上网方式与费用问题作出研究:
(1)分别写出三种上网方式中所用资费与时间的函数解析式;
(2)在同一坐标系内分别画出三种方式所需资费与时间的函数图象;
(3)根据你的研究,请给刘先生一个合理化的建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com