
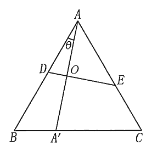
【题目】如图所示,一张形状为等边三角形![]() 的纸片,边长为8,将它对折,使顶点
的纸片,边长为8,将它对折,使顶点![]() 落在边
落在边![]() 上,当点
上,当点![]() 沿着
沿着![]() 从点
从点![]() 到点
到点![]() 移动时,求折痕长的最大值及最小值.
移动时,求折痕长的最大值及最小值.
科目:高中数学 来源: 题型:
【题目】为了防止受到核污染的产品影响我国民众的身体健康,要求产品在进入市场前必须进行两轮核辐射检测,只有两轮都合格才能进行销售,否则不能销售.已知某产品第一轮检测不合格的概率为![]() ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为![]() ,两轮检测是否合格相互没有影响.若产品可以销售,则每件产品获利40元;若产品不能销售,则每件产品亏损80元.已知一箱中有4件产品,记一箱产品获利X元,则P(X≥-80)=________.
,两轮检测是否合格相互没有影响.若产品可以销售,则每件产品获利40元;若产品不能销售,则每件产品亏损80元.已知一箱中有4件产品,记一箱产品获利X元,则P(X≥-80)=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】辊子是客家传统农具,南方农民犁开田地后,仍有大的土块.农人便用六片叶齿组成辊轴,两侧装上木板,人跨开两脚站立,既能掌握平衡,又能增加重量,让牛拉动辊轴前进,压碎土块,以利于耕种.这六片叶齿又对应着菩萨六度,即布施持戒忍辱精进禅定与般若.若甲乙每人依次有放回地从这六片叶齿中随机取一片,则这两人选的叶齿对应的“度”相同的概率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 为椭圆
为椭圆![]() :
:![]() 的右焦点,过
的右焦点,过![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 、
、![]() 斜率的乘积为
斜率的乘积为![]() ,两直线
,两直线![]() ,
,![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() 、
、![]() 、
、![]() 、
、![]() 四点,求四边形
四点,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的某种产品成箱包装,每箱20件,每一箱产品在交付用户时,用户要对该箱中部分产品作检验.设每件产品为不合格品的概率都为![]() ,且各件产品是否合格相互独立.
,且各件产品是否合格相互独立.
(1)记某一箱20件产品中恰有2件不合格品的概率为![]() ,
,![]() 取最大值时对应的产品为不合格品概率为
取最大值时对应的产品为不合格品概率为![]() ,求
,求![]() ;
;
(2)现从某一箱产品中抽取3件产品进行检验,以(1)中确定的![]() 作为p的值,已知每件产品的检验费用为10元,若检验出不合格品,则工厂要对每件不合格品支付30元的赔偿费用,检验费用与赔偿费用的和记为
作为p的值,已知每件产品的检验费用为10元,若检验出不合格品,则工厂要对每件不合格品支付30元的赔偿费用,检验费用与赔偿费用的和记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com