把4名中学生分别推荐到3所不同的大学去学习.每个大学至少收一名.全部分完.不同的分配方案数为36．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

20．把4名中学生分别推荐到3所不同的大学去学习，每个大学至少收一名，全部分完，不同的分配方案数为36．

分析由题意知将4名中学生分别推荐到3所不同的大学去学习，每个大学至少收一名，需要先从4个人中选出2个作为一个元素看成整体，再把它同另外两个元素在三个位置全排列，根据分步乘法原理得到结果．

解答解：∵将4名中学生分别推荐到3所不同的大学去学习，每个大学至少收一名，
∴先从4个人中选出2个作为一个元素看成整体，
再把它同另外两个元素在三个位置全排列，共有C²₄A³₃=36．
故答案为：36．

点评本题考查排列组合及简单的计数问题，是一个基础题，本题又是一个易错题，排列容易重复，注意做到不重不漏．

练习册系列答案

开心快乐假期作业暑假作业西安出版社系列答案

学业考试综合练习册系列答案

名题训练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

12．在${（\sqrt{2}-\root{3}{3}）^{50}}$的展开式中有9项为有理数．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

11．

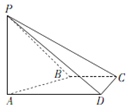如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AD∥BC，AD⊥CD，AD=2BC=2CD．
（1）在线段AD上确定一点M，使得平面PBM⊥平面PAD，并说明理由；
（2）若二面角P-CD-A的大小为45°，求二面角P-CD-A的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

8．已知随机变量ξ的分布列如图所示，则函数a=0.3，E（ξ）=1．

ξ	0	1	2
P	0.3	0.4	a

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

15．已知函数f（x）=Asin（ωx+φ）+b（$A＞0，ω＞0，|φ|＜\frac{π}{2}$）的图象上相邻的一个最大值点与对称中心分别为（$\frac{π}{18}$，3）、$（\frac{2π}{9}，0）$，则函数f（x）的单调增区间为（　　）

	A．	（$\frac{2kπ}{3}-\frac{π}{9}$，$\frac{2kπ}{3}+\frac{2π}{9}$），k∈Z		B．	（$\frac{2kπ}{3}$-$\frac{4π}{9}$，$\frac{2kπ}{3}$-$\frac{π}{9}$），k∈Z
	C．	（$\frac{2kπ}{3}$+$\frac{π}{18}$，$\frac{2kπ}{3}$+$\frac{7π}{18}$），k∈Z		D．	（$\frac{2kπ}{3}$-$\frac{7π}{18}$，$\frac{2kπ}{3}-\frac{π}{18}$），k∈Z

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

5．已知函数f（x）=$\frac{6}{x-1}$，
（1）判断函数f（x）在（1，+∞）上的单调性并用单调性的定义证明；
（2）若x∈[2，4]，求函数f（x）值域．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

12．

心理健康教育老师对某班50个学生进行了心里健康测评，测评成绩满分为100分．成绩出来后，老师对每个成绩段的人数进行了统计，并得到如图4所示的频率分布直方图．
（1）求a，并从频率分布直方图中求出成绩的众数和中位数；
（2）若老师从60分以下的人中选两个出来与之聊天，则这两人一个在（40，50]这一段，另一个在（50，60]这一段的概率是多少？

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

8．