Question

对于每个正整数n，将n表示成2的非负整数次方的和，令f(n)为正整数n的不同表示法的个数．

如果两个表示法的差别仅在于它们中各个数相加的次序不同，这两个表示法就被视为是相同的．例如，f(4)＝4，因为4恰有下列四种表示法：4；2＋2；2＋1＋1；1＋1＋1＋1．

Answer 1

证明：对于任意一个大于1的奇数n＝2k＋1，n的任一表示中必含一个1．去掉这个1就得到2k的一个表示．反之，给2k的任一表示加上一个1就得到2k＋1的一个表示．这显然是2k＋1和2k的表示之间的一个一一对应．从而有如下递归式：

f(2k＋1)＝f(2k)                                (1)

对于任意正偶数n＝2k，其表示可以分为两类：含有1的与不含1的．对于前者，去掉一个1就得到2k－1的一个表示；对于后者，将每一项除以2，就得到k的一个表示．这两种变换都是可逆的，从而都是一一对应．于是得到第二个递归式：

f(2k)＝f(2k－1)＋f(k)                       (2)

(1)、(2)式对于任意k≥1都成立．显然f(1)＝1．定义f(0)＝1，则(1)式对于k＝0也成立．根据(1)、(2)式，函数f是不减的．

由(1)式，可以将(2)式中的f(2k－1)换成f(2k－2)，得到f(2k)－f(2k－2)＝f(k)，k＝1，2，3，…，给定任一正整数n≥1，将上式对于k＝1，2，…，n求和，得到

f(2n)＝f(0)＋f(1)＋…＋f(n)，n＝1，2，3，…(3)

下面先证明上界，在(3)式中，右端所有的项都不大于最后一项，对于n≥2，2＝f(2)≤f(n)．于是有

f(2n)＝2＋(f(2)＋…＋f(n))≤2＋(n－1)f(n)

≤f(n)＋(n－1)f(n)＝nf(n)

n＝2，3，4，…从而得到

f(2ⁿ)≤2^n－1?f(2^n－1)≤2^n－1?2^n－2?f(2^n－1)

≤2^n－1?2^n－2?2^n－3?f(2^n－3)≤…

≤2^{(n－1)＋(n－2)＋…＋1}?f(2)＝2^n(n－1)/2?2

为了证明下界，我们先证明对于具有相同奇偶性的正整数b≥a≥0，有如下不等式成立：

f(b＋1)－f(b)≥f(a＋1)－f(a)                           (4)

事实上，如果a、b同为偶数，则由(1)式知上式两端均等于0．而当a、b同为奇数时，由(2)式知f(b＋1)－f(b)＝f(b＋1)/2)，f(a＋1)－f(a)＝f((a＋1)/2)．由函数f是不减的即得不等式(4)成立．

任取正整数r≥k≥1，其中r为偶数，在(4)式中依次令a＝r－j，b＝r＋j，j＝0，1，…，k－1．然后将这些不等式加起来，得到

f(r＋k)－f(r)≥f(r＋1)－f(r－k＋1)

因为r是偶数，所以f(r＋1)＝f(r)．从而

f(r＋k)＋f(r－k＋1)≥2f(r)，k＝1，…，r

对于k＝1，…，r，将上述不等式相加，即得

f(1)＋f(2)＋…＋f(2r)≥2rf(r)

根据(3)式，上式左端等于f(4r)－1．从而对于任意偶数r≥2，f(4r)＞2rf(r)＋1＞2rf(r)．取r＝2^m－2即得

f(2^m)≥2^m－1f(2^m－2)                                     (5)

要使r＝2^m－2为偶数，m须为大于2的整数，但是(5)式对于m＝2也成立．

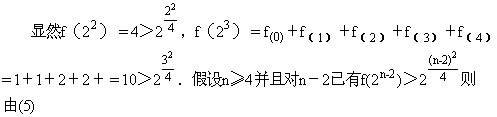
因此对一切n≥2下界成立．