
【题目】如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.
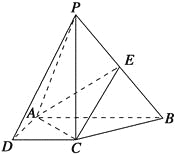
(1)求证:平面EAC⊥平面PBC;
(2)若二面角P-AC-E的余弦值为![]() ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】(1)∵PC⊥平面ABCD,AC平面ABCD,∴AC⊥PC.∵AB=2,AD=CD=1,∴AC=BC=![]() .
.
∴AC2+BC2=AB2.∴AC⊥BC.
又BC∩PC=C,∴AC⊥平面PBC.
∵AC平面EAC,
∴平面EAC⊥平面PBC.
(2)如图,以点C为原点, ![]() ,
, ![]() ,
, ![]() 分别为x轴、y轴、z轴正方向,建立空间直角坐标系,
分别为x轴、y轴、z轴正方向,建立空间直角坐标系,
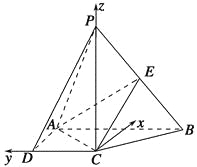
则C(0,0,0),A(1,1,0),B(1,-1,0),设P(0,0,a)(a>0),
则E![]() ,
, ![]() =(1,1,0),
=(1,1,0), ![]() =(0,0,a),
=(0,0,a), ![]() =
=![]() .取m=(1,-1,0),则m·
.取m=(1,-1,0),则m·![]() =m·
=m·![]() =0,m为面PAC的法向量.设n=(x,y,z)为面EAC的法向量,则n·
=0,m为面PAC的法向量.设n=(x,y,z)为面EAC的法向量,则n·![]() =n·
=n·![]() =0,即
=0,即![]() 取x=a,y=-a,z=-2,则n=(a,-a,-2),依题意,|cos〈m,n〉|=
取x=a,y=-a,z=-2,则n=(a,-a,-2),依题意,|cos〈m,n〉|=![]() =
=![]() =
=![]() ,则a=2.于是n=(2,-2,-2),
,则a=2.于是n=(2,-2,-2), ![]() =(1,1,-2).设直线PA与平面EAC所成角为θ,则sinθ=|cos〈
=(1,1,-2).设直线PA与平面EAC所成角为θ,则sinθ=|cos〈![]() ,n〉|=
,n〉|=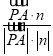 =
=![]() ,即直线PA与平面EAC所成角的正弦值为
,即直线PA与平面EAC所成角的正弦值为![]()


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln x-ax(a∈R)(e=2.718 28…是自然对数的底数).
(1)判断f(x)的单调性;
(2)当f(x)<0在(0,+∞)上恒成立时,求a的取值范围;
(3)证明:当x∈(0,+∞)时,![]() (1+x)
(1+x) ![]() <e.
<e.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示是某企业2010年至2016年污水净化量(单位: 吨)的折线图.
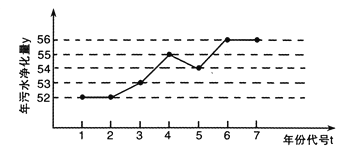
注: 年份代码1-7分别对应年份2010-2016.
(1)由折线图看出,可用线性回归模型拟合![]() 和
和![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程,预测
的回归方程,预测![]() 年该企业污水净化量;
年该企业污水净化量;
(3)请用数据说明回归方程预报的效果.
附注: 参考数据:![]() ;
;
参考公式:相关系数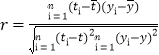 ,回归方程
,回归方程![]() 中斜率和截距的最小;
中斜率和截距的最小;
二乘法估汁公式分别为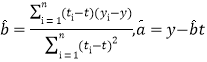 ;
;
反映回归效果的公式为: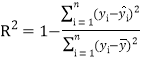 ,其中
,其中![]() 越接近于
越接近于![]() ,表示回归的效果越好.
,表示回归的效果越好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究家用轿车在高速公路上的车速情况,交通部门对100名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在55名男性驾驶员中,平均车速超过100km/h的有40人,不超过100km/h的有15人.在45名女性驾驶员中,平均车速超过100km/h的有20人,不超过100km/h的有25人.
(1)完成下面的列联表,并判断是否有99.5%的把握认为平均车速超过100km/h的人与性别有关.
平均车速超过 100km/h人数 | 平均车速不超过 100km/h人数 | 合计 | |
男性驾驶员人数 | |||
女性驾驶员人数 | |||
合计 |
(2)以上述数据样本来估计总体,现从高速公路上行驶的大量家用轿车中随机抽取3辆,记这3辆车中驾驶员为男性且车速超过100km/h的车辆数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式与数据: 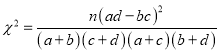 ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
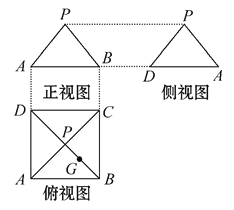
(1)根据三视图,画出该几何体的直观图.
(2)在直观图中,①证明:PD∥平面AGC;
②证明:平面PBD⊥平面AGC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com