【题目】已知椭圆
过点
，离心率为
，
分别为左右焦点.
（1）求椭圆
的标准方程；
（2）若
上存在两个点
，椭圆上有两个点
满足
三点共线，
三点共线，且
，求四边形
面积的取值范围.
科目：高中数学 来源： 题型：
【题目】如图，有一段河流，河的一侧是以O为圆心，半径为
米的扇形区域OCD，河的另一侧是一段笔直的河岸l，岸边有一烟囱AB（不计B离河岸的距离），且OB的连线恰好与河岸l垂直，设OB与圆弧
的交点为E．经测量，扇形区域和河岸处于同一水平面，在点C，点O和点E处测得烟囱AB的仰角分别为
，
和
．
（1）求烟囱AB的高度；
（2）如果要在CE间修一条直路，求CE的长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某飞机失联，经卫星侦查，其最后出现在小岛
附近，现派出四艘搜救船
，为方便联络，船
始终在以小岛为圆心，100海里为半径的圆上，船构成正方形编队展开搜索，小岛在正方形编队外（如图）.设小岛到
的距离为
，
，
船到小岛的距离为
.
（1）请分别求关于
的函数关系式
，并分别写出定义域；
（2）当两艘船之间的距离是多少时搜救范围最大（即最大）？
查看答案和解析>>
科目：高中数学 来源： 题型：
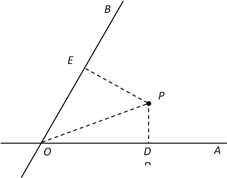
【题目】如图，
、
是两条公路（近似看成两条直线），
，在
内有一纪念塔
（大小忽略不计），已知到直线、的距离分别为
、
，=6千米，=12千米．现经过纪念塔修建一条直线型小路，与两条公路、分别交于点
、
．
（1）求纪念塔到两条公路交点
处的距离；
（2）若纪念塔为小路
的中点，求小路的长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的左、右焦点分别为
，点
也为抛物线
的焦点，过点的直线
交抛物线
于
两点.
（Ⅰ）若点
满足
，求直线的方程；
（Ⅱ）
为直线
上任意一点，过点
作
的垂线交椭圆
于
两点，求
的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线
（
）.
（1）证明：直线
过定点；
（2）若直线不经过第四象限，求
的取值范围；
（3）若直线
轴负半轴于
，交
轴正半轴于
，△
的面积为
（
为坐标原点），求的最小值，并求此时直线的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为增强市民的节能环保意识，郑州市面向全市征召义务宣传志愿者，从符合条件的500名志愿者中随机抽取100名，其年龄频率分布直方图如图所示，其中年龄分组区是：
．
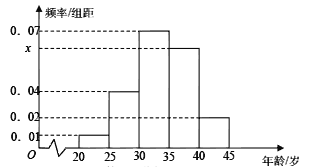
（Ⅰ）求图中
的值，并根据频率分布直方图估计这500名志愿者中年龄在
岁的人数；
（Ⅱ）在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动，再从这10名志愿者中选取3名担任主要负责人．记这3名志愿者中“年龄低于35岁”的人数为
，求
的分布列及数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1，在边长为1的等边三角形ABC中，D，E分别是AB，AC边上的点，AD=AE，F是BC的中点，AF与DE交于点G，将△ABF沿AF折起，得到如图2所示的三棱锥A﹣BCF，其中BC=
．
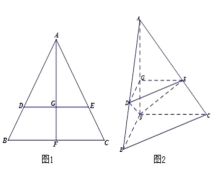
（Ⅰ）证明：DE∥平面BCF；
（Ⅱ）证明：CF⊥平面ABF；
（Ⅲ）当AD=
时，求三棱锥F﹣DEG的体积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
