
分析 直接由计算器求出区间(0,1)的端点出的函数值及其区间中点处的函数值,直至区间端点差的绝对值满足精确度为止,则答案可求.
解答 解:f(x)=3x-$\sqrt{2-x}$,因为,f(0)=30-$\sqrt{2}$<0,f(1)=3-1>0,所以函数在(0,1)内存在零点,即方程3x-$\sqrt{2-x}$=0在(0,1)内有实数根.
取(0,1)的中点0.5,经计算f(0.5)>0,又f(0)<0,所以方程3x-$\sqrt{2-x}$=0在(0.0.5)内有实数根.
如此继续下去,得到方程的一个实数根所在的区间,如下表:
| (a,b) | (a,b) 的中点 | f(a) | f(b) | f($\frac{a+b}{2}$ ) |
| (0,1) | 0.5 | f(0)<0 | f(1)>0 | f(0.5)>0 |
| (0,0.5) | 0.25 | f(0)<0 | f(0.5)>0 | f(0.25)<0 |
| (0.25,0.5) | 0.375 | f(0.25)<0 | f(0.5)>0 | f(0.375)>0 |
| (0.25,0.375) | 0.3125 | f(0.25)<0 | f(0.375)>0 | f(0.3125)>0 |
点评 本题主要考查用二分法求方程的近似解的方法和步骤,函数的零点与方程的根的关系,属于基础题


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
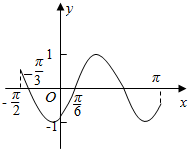 若函数y=sin(ωx-φ)(ω>0,|φ|<π)在区间$[{-\frac{π}{2},π}]$的简图如图所示,则ω,φ的值分别是( )
若函数y=sin(ωx-φ)(ω>0,|φ|<π)在区间$[{-\frac{π}{2},π}]$的简图如图所示,则ω,φ的值分别是( )| A. | $ω=2,φ=\frac{π}{3}$ | B. | $ω=2,φ=-\frac{2π}{3}$ | C. | $ω=\frac{1}{2},φ=\frac{π}{3}$ | D. | $ω=\frac{1}{2},φ=-\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=lgx2,g(x)=2lgx | B. | f(x)=1,g(x)=x0 | ||
| C. | $f(x)=\sqrt{x^2},g(x)={(\sqrt{x})^2}$ | D. | $f(x)=x,g(x)={log_a}{a^x}(a>0且a≠1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | [4,8) | C. | (4,8) | D. | (1,8) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com