
 平罗中学从高二年级参加生物考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60),…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
平罗中学从高二年级参加生物考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60),…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:分析 (1)由频率分布图中小矩形的面积和为1,能求出得成绩落在[70,80)上的频率,由此能补全这个频率分布直方图.
(2)由频率分布直方图能估计这次考试的及格率和平均分.
解答 解:(1)由频率分布图得成绩落在[70,80)上的频率为:
1-(0.010+0.015+0.015+0.025+0.005)×10=0.3.
补全这个频率分布直方图,如下图: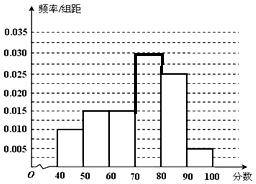
(2)由频率分布直方图估计这次考试的及格率为:
(0.015+0.030+0.025+0.005)×10×100%=75%.
平均分为:0.01×10×45+0.015×10×55+0.015×10×65+0.030×10×75+0.025×10×85+0.005×10×95=71.
点评 本题考查频率、及格率、平均分的求法,是基础题,解题时要认真审题,注意频率分布直方图的性质的合理运用.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | {-2,1,2} | B. | {-2,2} | C. | {1,2} | D. | {1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若x2≥1,则-1≥x≥1 | B. | 若1≥x≥-1,则x2≥1 | ||
| C. | 若x≤-1或x≥1,则x2≥1 | D. | 若x2≥1,则x≤-1或x≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ①② | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com