
【题目】如图,在三棱锥P-ABC中,AC⊥BC,且,AC=BC=2,D,E分别为AB,PB中点,PD⊥平面ABC,PD=3.
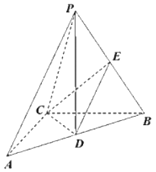
(1)求直线CE与直线PA夹角的余弦值;
(2)求直线PC与平面DEC夹角的正弦值.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知平行于
中,已知平行于![]() 轴的动直线
轴的动直线![]() 交抛物线
交抛物线![]() :
: ![]() 于点
于点![]() ,点
,点![]() 为
为![]() 的焦点.圆心不在
的焦点.圆心不在![]() 轴上的圆
轴上的圆![]() 与直线
与直线![]() ,
, ![]() ,
, ![]() 轴都相切,设
轴都相切,设![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,过
,过![]() 且垂直于
且垂直于![]() 的直线为
的直线为![]() ,直线
,直线![]() ,
, ![]() 分别与
分别与![]() 轴相交于点
轴相交于点![]() ,
, ![]() .当线段
.当线段![]() 的长度最小时,求
的长度最小时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,定义![]() 为两点
为两点![]() ,
,![]() 之间的“折线距离”.则下列命题中:
之间的“折线距离”.则下列命题中:
①若![]() 点在线段
点在线段![]() 上,则有
上,则有![]()
②若点![]() ,
,![]() ,
,![]() 是三角形的三个顶点,则有
是三角形的三个顶点,则有![]() .
.
③到![]() 两点的“折线距离”相等的点的轨迹是直线
两点的“折线距离”相等的点的轨迹是直线![]() .
.
④若![]() 为坐标原点,
为坐标原点,![]() 在直线
在直线![]() 上,则
上,则![]() 的最小值为
的最小值为![]() .
.
真命题的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为庆祝新中国成立七十周年,巴蜀中学将举行“歌唱祖国,喜迎国庆”歌咏比赛活动,《歌唱祖国》,《精忠报国》,《我和我的祖国》等一系列歌曲深受同学们的青睐,高二某班级就该班是否选择《精忠报国》作为本班参赛曲目进行投票表决,投票情况如下表.
小组 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
赞成人数 | 4 | 5 | 6 | 6 | 5 | 6 | 4 | 3 |
总人数 | 7 | 7 | 8 | 8 | 7 | 7 | 6 | 6 |
(1)若从第1小组和第8小组的同学中各随机选取2人进行调查,求所选取的4人中至少有2人赞成《精忠报国》作为本班参赛曲目的概率;
(2)若从第5小组和第7小组的同学中各随机选取2人进行调查,记选取的4人中不赞成《精忠报国》作为本班参赛曲目的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点曲线
的焦点曲线![]() 的一个焦点,
的一个焦点, ![]() 为坐标原点,点
为坐标原点,点![]() 为抛物线
为抛物线![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 轴的平行线交抛物线的准线于
轴的平行线交抛物线的准线于![]() ,直线
,直线![]() 交抛物线于点
交抛物线于点![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)求证:直线![]() 过定点
过定点![]() ,并求出此定点的坐标.
,并求出此定点的坐标.
【答案】(I)![]() ;(II)证明见解析.
;(II)证明见解析.
【解析】试题分析:(Ⅰ)将曲线![]() 化为标准方程,可求得
化为标准方程,可求得![]() 的焦点坐标分别为
的焦点坐标分别为![]() ,可得
,可得![]() ,所以
,所以![]() ,即抛物线的方程为
,即抛物线的方程为![]() ;(Ⅱ)结合(Ⅰ),可设
;(Ⅱ)结合(Ⅰ),可设![]() ,得
,得 ,从而直线
,从而直线![]() 的方程为
的方程为![]() ,联立直线与抛物线方程得
,联立直线与抛物线方程得![]() ,解得
,解得![]() ,直线
,直线![]() 的方程为
的方程为 ,整理得
,整理得![]() 的方程为
的方程为![]() ,此时直线恒过定点
,此时直线恒过定点![]() .
.
试题解析:(Ⅰ)由曲线![]() ,化为标准方程可得
,化为标准方程可得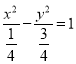 , 所以曲线
, 所以曲线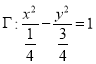 是焦点在
是焦点在![]() 轴上的双曲线,其中
轴上的双曲线,其中![]() ,故
,故![]() ,
, ![]() 的焦点坐标分别为
的焦点坐标分别为![]() ,因为抛物线的焦点坐标为
,因为抛物线的焦点坐标为![]() ,由题意知
,由题意知![]() ,所以
,所以![]() ,即抛物线的方程为
,即抛物线的方程为![]() .
.
(Ⅱ)由(Ⅰ)知抛物线![]() 的准线方程为
的准线方程为![]() ,设
,设![]() ,显然
,显然![]() .故
.故 ,从而直线
,从而直线![]() 的方程为
的方程为![]() ,联立直线与抛物线方程得
,联立直线与抛物线方程得![]() ,解得
,解得![]()
①当![]() ,即
,即![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,
,
②当![]() ,即
,即![]() 时,直线
时,直线![]() 的方程为
的方程为 ,整理得
,整理得![]() 的方程为
的方程为![]() ,此时直线恒过定点
,此时直线恒过定点![]() ,
, ![]() 也在直线
也在直线![]() 的方程为
的方程为![]() 上,故直线
上,故直线![]() 的方程恒过定点
的方程恒过定点![]() .
.
【题型】解答题
【结束】
21
【题目】已知函数![]() ,
, ![]()
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)若![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若数列![]() 满足
满足![]() ,
, ![]() ,记
,记![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
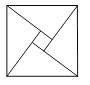
【题目】第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如图所示,会标是由四个全等的直角三角形与一个小正方形拼成的一个大正方形.如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为![]() ,那么
,那么![]() _____________.
_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com