
ĄūĖâÄŋĄŋ―üžļÄęĢŽĩįÉĖÐÐŌĩĩÄÅîēŠ·ĒÕđīøķŊÁËŋėĩÝŌĩĩÄŅļËŲÔöģĪĢŽŋėĩÝđŦËūĀŋĘÕžÛļņŌŧ°ãĘĮēÉÓÃĄ°ĘŨÖØ+ÐøÖØĄąĩĞƞ۷―Ę―.ĘŨÖØĘĮÖļŨîĩÍĩĞƷŅÖØÁŋĢŽÐøÖØĘĮÖļģŽđýĘŨÖØēŋ·ÖĩĞƷŅÖØÁŋĢŽēŧÂúŌŧđŦ―ï°īŌŧđŦ―ïžÆ·Ņ.ÄģŋėĩÝÍøĩã―ŦŋėžþĩÄĀŋĘÕžÛļņķĻΊĘŨÖØĢĻēŧģŽđýŌŧđŦ―ïĢĐ8ÔŠĢŽÐøÖØ2ÔŠ/đŦ―ïĢĻĀýČįĢŽČôŌŧļöŋėžþĩÄÖØÁŋĘĮ0.6đŦ―ïĢŽ°ī8ÔŠžÆ·ŅĢŧČôŌŧļöŋėžþĩÄÖØÁŋĘĮ1.4đŦ―ïĢŽ°ī![]() ÔŠ
ÔŠ![]() ÔŠ
ÔŠ![]() ÔŠžÆ·ŅĢĐ.ļųūÝĀúĘ·ĘýūÝĢŽĩÃĩ―ļÃÍøĩãĀŋĘÕŋėžþÖØÁŋĩÄÆĩÂĘ·ÖēžÖą·―ÍžČįÏÂÍžËųĘū
ÔŠžÆ·ŅĢĐ.ļųūÝĀúĘ·ĘýūÝĢŽĩÃĩ―ļÃÍøĩãĀŋĘÕŋėžþÖØÁŋĩÄÆĩÂĘ·ÖēžÖą·―ÍžČįÏÂÍžËųĘū
ĢĻ1ĢĐļųūÝŅųąūđĀžÆŨÜĖåĩÄËžÏëĢŽ―ŦÆĩÂĘĘÓŨũļÅÂĘĢŽĮóļÃÍøĩãĀŋĘÕŋėžþĩÄÆ―ūųžÛļņĢŧ
ĢĻ2ĢĐΊÁËŧņĩÃļüīóĩÄĀûČóĢŽļÃÍøĩãķÔĄ°ŌŧĖėÖÐĘÕ·ĒŌŧžþŋėĩÝĩÄÆ―ūųģÉąū![]() ĢĻĩĨÎŧĢšÔŠĢĐÓëĩąĖėĀŋĘÕĩÄŋėĩÝžþĘý
ĢĻĩĨÎŧĢšÔŠĢĐÓëĩąĖėĀŋĘÕĩÄŋėĩÝžþĘý![]() ĢĻĩĨÎŧĢš°ŲžþĢĐ
ĢĻĩĨÎŧĢš°ŲžþĢĐ![]() ÖŪžäĩÄđØÏĩĄą―øÐÐĩũēéŅÐūŋĢŽĩÃĩ―ÏāđØĘýūÝČįÏÂąíĢš
ÖŪžäĩÄđØÏĩĄą―øÐÐĩũēéŅÐūŋĢŽĩÃĩ―ÏāđØĘýūÝČįÏÂąíĢš
ÃŋĖėĀŋĘÕŋėĩÝžþĘý | 2 | 3 | 4 | 5 | 8 |
ÃŋžþŋėĩÝĩÄÆ―ūųģÉąū | 5.6 | 4.8 | 4.4 | 4.3 | 4.1 |
ļųūÝŌÔÉÏĘýūÝĢŽžžĘõČËÔą·ÖąðļųūÝžŨĄĒŌŌÁ―ÖÖēŧÍŽĩÄŧØđéÄĢÐÍĢŽĩÃĩ―Á―ļöŧØđé·―ģĖĢš
·―ģĖžŨĢš![]() ĢŽ·―ģĖŌŌĢš
ĢŽ·―ģĖŌŌĢš![]() .
.
ĒŲΊÁËÆĀžÛÁ―ÖÖÄĢÐÍĩÄÄâšÏЧđûĢŽļųūÝÉÏąíĘýūÝšÍÏāÓĶŧØđé·―ģĖĢŽ―ŦŌÔÏÂąíļņĖîÐīÍęÕûĢĻ―áđûąĢÁôŌŧÎŧÐĄĘýĢĐĢŽ·ÖąðžÆËãÄĢÐÍžŨÓëÄĢÐÍŌŌĩÄēÐēîÆ―·―šÍ![]() ĢŽ
ĢŽ![]() ĢŽēĒŌĀīËÅÐķÏÄÄļöÄĢÐÍĩÄÄâšÏЧđûļüšÃĢĻąļŨĒĢš
ĢŽēĒŌĀīËÅÐķÏÄÄļöÄĢÐÍĩÄÄâšÏЧđûļüšÃĢĻąļŨĒĢš![]() ģÆΊÏāÓĶÓÚĩã
ģÆΊÏāÓĶÓÚĩã![]() ĩÄēÐēîĢŽēÐēîÆ―·―šÍ
ĩÄēÐēîĢŽēÐēîÆ―·―šÍ![]() Ģŧ
Ģŧ
ÃŋĖėĀŋĘÕŋėĩÝžþĘý | 2 | 3 | 4 | 5 | 8 | |
ÃŋĖėŋėĩÝĩÄÆ―ūųģÉąū | 5.6 | 4.8 | 4.4 | 4.3 | 4.1 | |
ÄĢÐÍžŨ | ÔĪąĻÖĩ | 5.2 | 5.0 | 4.8 | ||
ēÐēî |
| 0.2 | 0.4 | |||
ÄĢÐÍŌŌ | ÔĪąĻÖĩ | 5.5 | 4.8 | 4.5 | ||
ÔĪąĻÖĩ |
| 0 | 0.1 | |||
ĒÚÔĪžÆļÃÍøĩã―ņÄę6ÔÂ25ČÕĢĻķËÎį―ÚĢĐŌŧĖėŋÉŌÔĀŋĘÕ1000žþŋėĩÝĢŽĘÔļųūÝĒŲÖÐČ·ķĻĩÄÄâšÏЧđû―ÏšÃĩÄŧØđéÄĢÐÍđĀžÆļÃÍøĩãĩąĖėĩÄŨÜĀûČóĢĻŨÜĀûČó=ĢĻÆ―ūųžÛļņ-Æ―ūųģÉąūĢĐĄÁŨÜžþĘýĢĐ.
Ąūīð°ļĄŋĢĻ1ĢĐ![]() ÔŠĢĻ2ĢĐĒŲĖîąížû―âÎöĢŧ
ÔŠĢĻ2ĢĐĒŲĖîąížû―âÎöĢŧ![]() Ģŧ
Ģŧ![]() ĢŧÄĢÐÍŌŌĩÄÄâšÏЧđû―ÏšÃĒÚ
ĢŧÄĢÐÍŌŌĩÄÄâšÏЧđû―ÏšÃĒÚ![]() ÔŠ
ÔŠ
Ąū―âÎöĄŋ
ĢĻ1ĢĐļųūÝÆĩÂĘ·ÖēžÖą·―ÍžĩÃģöŋėžþžÛļņĩÄÆĩÂĘ·ÖēžąíĢŽÔŲžÆËãÆ―ūųžÛļņĢŧ
ĢĻ2ĢĐĒŲ·Öąð°Ņ![]() īúČëÁ―ÄĢÐÍ·―ģĖĢŽžÆËãÔĪąĻÖĩšÍēÐēîÆ―·―šÍĢŧ
īúČëÁ―ÄĢÐÍ·―ģĖĢŽžÆËãÔĪąĻÖĩšÍēÐēîÆ―·―šÍĢŧ
ĒÚ°Ņ![]() īúČëŧØđé·―ģĖĢŽĩÃģöÆ―ūųģÉąūĢŽÔŲžÆËãĀûČóĢŪ
īúČëŧØđé·―ģĖĢŽĩÃģöÆ―ūųģÉąūĢŽÔŲžÆËãĀûČóĢŪ
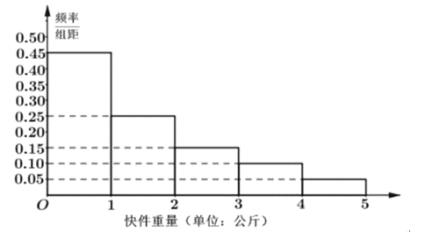
―âĢšĢĻ1ĢĐļųūÝĀŋĘÕŋėžþÖØÁŋĩÄÆĩÂĘ·ÖēžÖą·―ÍžĢŽĩÃĩ―ÆäžÛļņĩÄÆĩÂĘ·ÖēžąíČįÏÂĢš
žÛļņ | 8 | 10 | 12 | 14 | 16 |
ÆĩÂĘ | 0.45 | 0.25 | 0.15 | 0.1 | 0.05 |
ËųŌÔÆ―ūųžÛļņΊ![]()
![]() ÔŠ.
ÔŠ.
ĢĻ2ĢĐĒŲąíÖÐĘýūÝĖîÐīČįÏÂĢš
ÃŋĖėĀŋĘÕŋėĩÝžþĘý | 2 | 3 | 4 | 5 | 8 | |
ÃŋžþŋėĩÝĩÄÆ―ūųģÉąū | 5.6 | 4.8 | 4.4 | 4.3 | 4.1 | |
ÄĢÐÍžŨ | ÔĪąĻÖĩ | 5.2 | 5.0 | 4.8 | 4.6 | 4.0 |
ēÐēî |
| 0.2 | 0.4 | 0.3 |
| |
ÄĢÐÍŌŌ | ÔĪąĻÖĩ | 5.5 | 4.8 | 4.5 | 4.3 | 4.0 |
ēÐēî |
| 0 | 0.1 | 0 |
| |
žÆËãŋÉĩÃĢš![]() Ģŧ
Ģŧ
![]() .
.
ŌōΊ![]() ĢŽËųŌÔÄĢÐÍŌŌĩÄÄâšÏЧđû―ÏšÃ.
ĢŽËųŌÔÄĢÐÍŌŌĩÄÄâšÏЧđû―ÏšÃ.
ĒÚÄĢÐÍŌŌĩÄŧØđé·―ģĖΊ![]() ĢŽ
ĢŽ
ĩąŌŧĖėĀŋĘÕžþĘýΊ1000ĘąĢŽÔōĘÕ·ĒŌŧžþŋėĩÝĩÄÆ―ūųģÉąūΊ![]() ĢŽ
ĢŽ
ŋÉŌÔđĀžÆļÃÍøĩãĩąĖėĩÄŨÜĀûČóΊ![]() ÔŠ.
ÔŠ.



| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
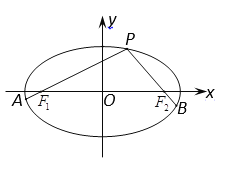
ĄūĖâÄŋĄŋÕýËÄĀâŨķPĐABCDĩÄĩŨÃæąßģĪΊ2,ēāĀâģĪΊ2![]() ,đýĩãAŨũŌŧļöÓëēāĀâPCīđÖąĩÄÆ―ÃæĶÁ,ÔōÆ―ÃæĶÁąŧīËÕýËÄĀâŨķËų―ØĩÄ―ØÃæÃæŧýΊ_____,Æ―ÃæĶÁ―ŦīËÕýËÄĀâŨķ·ÖģÉĩÄÁ―ēŋ·ÖĖåŧýĩÄąČÖĩΊ_____.
,đýĩãAŨũŌŧļöÓëēāĀâPCīđÖąĩÄÆ―ÃæĶÁ,ÔōÆ―ÃæĶÁąŧīËÕýËÄĀâŨķËų―ØĩÄ―ØÃæÃæŧýΊ_____,Æ―ÃæĶÁ―ŦīËÕýËÄĀâŨķ·ÖģÉĩÄÁ―ēŋ·ÖĖåŧýĩÄąČÖĩΊ_____.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÍÖÔē![]() ĩÄŨóĄĒÓŌ―đĩã·ÖąðΊ
ĩÄŨóĄĒÓŌ―đĩã·ÖąðΊ![]() ĢŽĩã
ĢŽĩã![]() ÔÚÍÖÔēÉÏĢŽÖąÏß
ÔÚÍÖÔēÉÏĢŽÖąÏß![]() ÓëÍÖÔēĩÄÁíŌŧļö―ŧĩã·ÖąðΊ
ÓëÍÖÔēĩÄÁíŌŧļö―ŧĩã·ÖąðΊ![]() .
.
ĢĻ1ĢĐČô![]() ĩãŨøąęΊ
ĩãŨøąęΊ![]() ĢŽĮŌ
ĢŽĮŌ![]() ĢŽĮóÍÖÔēĩÄ·―ģĖĢŧ
ĢŽĮóÍÖÔēĩÄ·―ģĖĢŧ
ĢĻ2ĢĐÉč![]() ĢŽ
ĢŽ![]() ĢŽĮóÖĪĢš
ĢŽĮóÖĪĢš![]() ΊķĻÖĩ.
ΊķĻÖĩ.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠĮúÏß![]() ĩÄžŦŨøąę·―ģĖĘĮ
ĩÄžŦŨøąę·―ģĖĘĮ![]() ĢŽŌÔžŦĩãΊÔĩãĢŽžŦÖáΊ
ĢŽŌÔžŦĩãΊÔĩãĢŽžŦÖáΊ![]() ÖáĩÄÕý°ëÖáĢŽ―ĻÁĒÆ―ÃæÖą―ĮŨøąęÏĩĢŽÖąÏß
ÖáĩÄÕý°ëÖáĢŽ―ĻÁĒÆ―ÃæÖą―ĮŨøąęÏĩĢŽÖąÏß![]() đýĩã
đýĩã![]() ĢŽĮãÐą―ĮΊ
ĢŽĮãÐą―ĮΊ![]() ĢŪ
ĢŪ
ĢĻ1ĢĐĮóĮúÏß![]() ĩÄÖą―ĮŨøąę·―ģĖÓëÖąÏßlĩÄēÎĘý·―ģĖĢŧ
ĩÄÖą―ĮŨøąę·―ģĖÓëÖąÏßlĩÄēÎĘý·―ģĖĢŧ
ĢĻ2ĢĐÉčÖąÏß![]() ÓëĮúÏß
ÓëĮúÏß![]() ―ŧÓÚ
―ŧÓÚ![]() ĢŽ
ĢŽ![]() Á―ĩãĢŽĮó
Á―ĩãĢŽĮó![]() ĩÄÖĩĢŪ
ĩÄÖĩĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋ2020ÄęČŦĮōąŽ·ĒÐÂđÚ·ÎŅŨĢŽČËļÐČūÁËÐÂđÚ·ÎŅŨēĄķūšóģĢžûĩÄšôÎüĩĀÖĒŨīÓÐĢš·ĒČČĄĒŋČËÔĄĒÆøīŲšÍšôÎüĀ§ÄŅĩČĢŽŅÏÖØĘąŧáÎĢž°ÉúÃüĢŪËæŨÅŌßĮéĩÄ·ĒÕđĢŽŨÔ2020Äę2ÔÂ5ČÕÆðĢŽÎäššīóÃæŧýĩÄąŽ·ĒÐÂđÚ·ÎŅŨĢŽÕþļŪΊÁËž°ĘąĘÕÖÎĮáÖĒļÐČūĩÄČšÖÚĢŽÖðē――ĻÁĒÆðÁË14žŌ·―ēÕŌ―ÔšĢŽÆäÖÐÎäššĖåÓýÖÐÐÄ·―ēÕŌ―ÔšīÓ2ÔÂ12ČÕŋŠēÕÖÁ3ÔÂ8ČÕąÕēÖĢŽĀÛžÆĘÕÖÎĮáÖĒŧžÕß1056ČËĢŪūÝēŋ·ÖÍģžÆļ÷―ēÕŌ―ÔšīÓ2ÔÂ26ČÕÖÁ3ÔÂ2ČÕĮáÖĒŧžÕßÖÎÓúģöēÖČËĘýĩÄÆĩĘýąíÓëÉĒĩãÍžČįÏÂĢš
ČÕÆÚ | 2.26 | 2.27 | 2.28 | 2.29 | 3.1 | 3.2 |
ÐōšÅ | 1 | 2 | 3 | 4 | 5 | 6 |
ģöēÖČËĘý | 3 | 8 | 17 | 31 | 68 | 168 |

ļųūÝÉĒĩãÍžšÍąíÖÐĘýūÝĢŽÄģŅÐūŋČËÔąķÔģöēÖČËĘý![]() ÓëČÕÆÚÐōšÅ
ÓëČÕÆÚÐōšÅ![]() ―øÐÐÁËÄâšÏ·ÖÎöĢŪīÓÉĒĩãÍžđÛēėŋÉĩÃĢŽŅÐūŋČËÔą·ÖąðÓÃÁ―ÖÖšŊĘýĒŲ
―øÐÐÁËÄâšÏ·ÖÎöĢŪīÓÉĒĩãÍžđÛēėŋÉĩÃĢŽŅÐūŋČËÔą·ÖąðÓÃÁ―ÖÖšŊĘýĒŲ![]() ĒÚ
ĒÚ![]() ·ÖÎöÆäÄâšÏЧđûĢŪÆäÏāđØÖļĘý
·ÖÎöÆäÄâšÏЧđûĢŪÆäÏāđØÖļĘý![]() ŋÉŌÔÅÐķÏÄâšÏЧđûĢŽR2Ô―īóÄâšÏЧđûÔ―šÃĢŪŌŅÖŠ
ŋÉŌÔÅÐķÏÄâšÏЧđûĢŽR2Ô―īóÄâšÏЧđûÔ―šÃĢŪŌŅÖŠ![]() ĩÄÏāđØÖļĘýΊ
ĩÄÏāđØÖļĘýΊ![]() ĢŪ
ĢŪ
ĢĻ1ĢĐĘÔļųūÝÏāđØÖļĘýÅÐķÏĢŪÉÏĘöÁ―ĀāšŊĘýĢŽÄÄŌŧĀāšŊĘýĩÄÄâšÏЧđûļüšÃĢŋĢĻŨĒĢšÏāđØÏĩĘý![]() ÓëÏāđØÖļĘýR2ÂúŨã
ÓëÏāđØÖļĘýR2ÂúŨã![]() ĢŽēÎŋžĘýūÝąíÖÐ
ĢŽēÎŋžĘýūÝąíÖÐ![]() ĢĐ
ĢĐ
ĢĻ2ĢĐĒŲļųūÝĢĻ1ĢĐÖÐ―áÂÛĢŽĮóÄâšÏЧđûļüšÃĩÄšŊĘý―âÎöĘ―ĢŧĢĻ―áđûąĢÁôÐĄĘýĩãšóČýÎŧĢĐ
ĒÚ3ÔÂ3ČÕĘĩžĘŨÜģöēÖČËĘýΊ216ČËĢŽ°īĒŲÖÐĩÄŧØđéÄĢÐÍžÆËãĢŽēîūāÓÐķāÉŲČËĢŋ
ĢĻļ―ĢšķÔÓÚŌŧŨéĘýūÝ![]() ĢŽÆäŧØđéÖąÏßΊ
ĢŽÆäŧØđéÖąÏßΊ![]()
ÏāđØÏĩĘý
ēÎŋžĘýūÝĢš
|
|
|
|
|
|
|
|
|
3.5 | 49.17 | 15.17 | 3.13 | 894.83 | 19666.83 | 10.55 | 13.56 | 3957083 |
![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŪ
ĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋđýÅŨÎïÏßy2=4xĩÄ―đĩãĩÄÖąÏßlÓëÅŨÎïÏß―ŧÓÚAĢŽBÁ―ĩãĢŽÉčĩãMĢĻ3ĢŽ0ĢĐ.ČôĄũMABĩÄÃæŧýΊ![]() ĢŽÔō|AB|=( )
ĢŽÔō|AB|=( )
A.2B.4C.![]() D.8
D.8
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÔēÖÜÂĘĶÐĘĮĘýŅ§ÖÐŌŧļö·ĮģĢÖØŌŠĩÄĘýĢŽĀúĘ·ÉÏÐíķāÖÐÍâĘýŅ§žŌĀûÓÃļũÖÖ°ė·ĻķÔĶÐ―øÐÐÁËđĀËã.ÏÖĀûÓÃÏÂÁÐĘĩŅéÎŌÃĮŌēŋÉķÔÔēÖÜÂĘ―øÐÐđĀËã.žŲÉčÄģÐĢđēÓÐŅ§ÉúNČËĢŽČÃÃŋČËËæŧúÐīģöŌŧķÔÐĄÓÚ1ĩÄÕýĘĩĘýaĢŽbĢŽÔŲÍģžÆģöaĢŽbĢŽ1ÄÜđđÔėČņ―ĮČý―ĮÐÎĩÄČËĘýMĢŽĀûÓÃËųŅ§ĩÄÓÐđØÖŠĘķĢŽÔōŋÉđĀžÆģöĶÐĩÄÖĩĘĮ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠšŊĘý![]() .
.
ĢĻ1ĢĐČôšŊĘý![]() ÔÚ
ÔÚ![]() īĶĩÄĮÐÏßÐąÂĘΊ2ĢŽĘÔĮóaĩÄÖĩž°īËĘąĩÄĮÐÏß·―ģĖĢŧ
īĶĩÄĮÐÏßÐąÂĘΊ2ĢŽĘÔĮóaĩÄÖĩž°īËĘąĩÄĮÐÏß·―ģĖĢŧ
ĢĻ2ĢĐČôšŊĘý![]() ÔÚĮøžä
ÔÚĮøžä![]() ĢĻÆäÖÐ
ĢĻÆäÖÐ![]() ĄÎŠŨÔČŧķÔĘýĩÄĩŨĘýĢĐÉÏÓÐÎĻŌŧĩÄÁãĩãĢŽĮóĘĩĘýaĩÄČĄÖĩ·ķΧ.
ĄÎŠŨÔČŧķÔĘýĩÄĩŨĘýĢĐÉÏÓÐÎĻŌŧĩÄÁãĩãĢŽĮóĘĩĘýaĩÄČĄÖĩ·ķΧ.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋΊÁËļüšÃĩØđáģđĩģĩÄĄ°ÎåÓýēĒūŲĄąĩÄ―ĖÓý·―ÕëĢŽÄģĘÐŌŠķÔČŦĘÐÖÐÐĄŅ§ÉúĄ°ĖåÄÜīïąęĄąĮéŋö―øÐÐÁË―âĢŽūöķĻÍĻđýËæŧúģéŅųŅĄÔņžļļöŅųąūÐĢķÔŅ§Éú―øÐÐĖåÄÜīïąęēâĘÔĢŽēĒđæķĻēâĘÔģÉžĻĩÍÓÚ60·ÖΊēŧšÏļņĢŽ·ņÔōΊšÏļņĢŽČôŅųąūÐĢŅ§ÉúēŧšÏļņČËĘýēŧģŽđýÆäŨÜČËĘýĩÄ5%ĢŽÔōļÃŅųąūÐĢĖåÄÜīïąęΊšÏļņ.ŌŅÖŠÄģŅųąūÐĢđēÓÐ1000ÃûŅ§ÉúĢŽÏÖīÓÖÐËæŧúģéČĄ40ÃûŅ§ÉúēΞÓĖåÄÜīïąęēâĘÔĢŽĘŨÏČ―ŦÕâ40ÃûŅ§ÉúËæŧú·ÖΊžŨĄĒŌŌÁ―ŨéĢŽÆäÖОŨŌŌÁ―ŨéŅ§ÉúČËĘýĩÄąČΊ3:2ĢŽēâĘÔšóĢŽÁ―ŨéļũŨÔĩÄģÉžĻÍģžÆČįÏÂĢšžŨŨéĩÄÆ―ūųģÉžĻΊ70ĢŽ·―ēîΊ16ĢŽŌŌŨéĩÄÆ―ūųģÉžĻΊ80ĢŽ·―ēîΊ36.
ĢĻ1ĢĐđĀžÆļÃŅųąūÐĢŅ§ÉúĖåÄÜēâĘÔĩÄÆ―ūųģÉžĻĢŧ
ĢĻ2ĢĐĮóļÃŅųąūÐĢ40ÃûŅ§ÉúēâĘÔģÉžĻĩÄąęŨžēîsĢŧ
ĢĻ3ĢĐžŲÉčļÃŅųąūÐĢĖåÄÜīïąęēâĘÔģÉžĻ·þīÓÕýĖŽ·Öēž![]() ĢŽÓÃŅųąūÆ―ūųĘý
ĢŽÓÃŅųąūÆ―ūųĘý![]() ŨũΊ
ŨũΊ![]() ĩÄđĀžÆÖĩ
ĩÄđĀžÆÖĩ![]() ĢŽÓÃŅųąūąęŨžēîsŨũΊ
ĢŽÓÃŅųąūąęŨžēîsŨũΊ![]() ĩÄđĀžÆÖĩ
ĩÄđĀžÆÖĩ![]() ĢŽĀûÓÃđĀžÆÖĩđĀžÆļÃŅųąūÐĢŅ§ÉúĖåÄÜīïąęēâĘÔĘĮ·ņšÏļņĢŋ
ĢŽĀûÓÃđĀžÆÖĩđĀžÆļÃŅųąūÐĢŅ§ÉúĖåÄÜīïąęēâĘÔĘĮ·ņšÏļņĢŋ
ĢĻŨĒĢš1.ąūĖâËųÓÐĘýūÝĩÄŨîšó―áđûķžūŦČ·ĩ―ÕûĘýĢŧ2ČôËæŧúąäÁŋz·þīÓÕýĖŽ·ÖēžĢŽÔō![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢĐ
ĢĐ
ēéŋīīð°ļšÍ―âÎö>>
°ŲķČÖÂÐÅ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com