练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数，其中，为自然对数的底数.

    （1）讨论的极值；

    （2）当且时，求证：.

    【答案】（1）当时，无极值；当时，的极大值为，无极小值.（2）证明见解析

    【解析】

    （1）求导得到，令，得，讨论，两种情况，计算得到答案.

    （2）证明得到，记，根据单调性得到，故，得到证明.

    （1），令，得.

    当，即时，在内恒成立，

    故在内单调递减，无极值.

    当，即时，由，得，

    由，得，

    ∴在内单调递增，在内单调递减，

    ∴在处取得极大值，且极大值为.

    综上所述，当时，无极值.

    当时，的极大值为，无极小值.

    （2）设，则，

    当时，，单调递增，故，即，

    ∴，∴，

    记，则，

    当时，；当时，，

    故在内单调递减，在内单调递增，从而，

    ∴.①

    由（1）知，当且时，，

    ∴，②

    由①②可知，.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某翻译处有8名翻译，其中有小张等3名英语翻译，小李等3名日语翻译，另外2名既能翻译英语又能翻译日语，现需选取5名翻译参加翻译工作，3名翻译英语，2名翻译日语，且小张与小李恰有1人选中，则有____种不同选取方法.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了打击海盗犯罪，甲、乙、丙三国海军进行联合军事演习，分别派出一艘军舰A，B，C.演习要求：任何时刻军舰A、B、C均不得在同一条直线上.

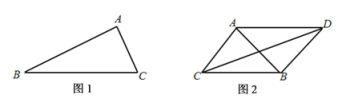
    （1）如图1，若演习过程中，A、B间的距离始终保持，B，C间的距离始终保持，求的最大值.

    （2）如图2，若演习过程中，A，C间的距离始终保持，B、C间的距离始终保持.且当变化时，模拟海盗船D始终保持：到B的距离与A、B间的距离相等，，与C在直线AB的两侧，求C与D间的最大距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列满足，且.

    （1）求数列的通项公式；

    （2）若数列的前项和为，且，，数列的前项和为，求满足的所有正整数的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】极坐标系中椭圆C的方程为，以极点为原点，极轴为轴非负半轴，建立平面直角坐标系，且两坐标系取相同的单位长度．

    （Ⅰ）求该椭圆的直角标方程，若椭圆上任一点坐标为，求的取值范围；

    （Ⅱ）若椭圆的两条弦，交于点，且直线与的倾斜角互补，求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直四棱柱中，四边形是平行四边形，且．

    （1）证明：平面；

    （2）若与平面所成的角为45°，是的中点，求异面直线与所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是等差数列的前n项和，，，是数列的前n项和，.

    （1）求数列和的通项公式；

    （2）设，数列的前n项和为，若只存在2个正整数n满足，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求的单调区间与极值；

    （2）当函数有两个极值点时，求实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近年来，随着“一带一路”倡议的推进，中国与沿线国家旅游合作越来越密切，中国到“一带一路”沿线国家的游客人也越来越多，如图是2013－2018年中国到“一带一路”沿线国家的游客人次情况，则下列说法正确的是（ ）

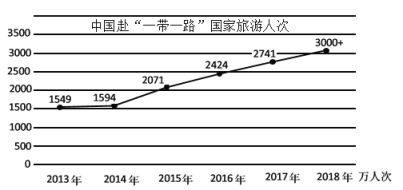
    ①2013－2018年中国到“一带一路”沿线国家的游客人次逐年增加

    ②2013－2018年这6年中，2014年中国到“一带一路”沿线国家的游客人次增幅最小

    ③2016－2018年这3年中，中国到“一带一路”沿线国家的游客人次每年的增幅基本持平

    A.①②③B.②③C.①②D.③

    查看答案和解析>>

    同步练习册答案