
【题目】已知点E(﹣2,0),点P时圆F:(x﹣2)2+y2=36上任意一点,线段EP的垂直平分线交FP于点M,点M的轨迹记为曲线C.
(Ⅰ)求曲线C的方程;
(Ⅱ)过F的直线交曲线C于不同的A、B两点,交y轴于点N,已知 ![]() =m
=m ![]() ,
, ![]() =n
=n ![]() ,求m+n的值.
,求m+n的值.
【答案】解:(Ⅰ)由题意知,|ME|+|MF|=|MP|+|MF|=r=6>|EF|=4,
故由椭圆定义知,点M的轨迹是以点E,F为焦点,长轴为6,焦距为4的椭圆,从而长半轴长为a=3,短半轴长为b= ![]() =
= ![]() ,
,
∴曲线C的方程为: ![]()
(Ⅱ)由题知F(2,0),
若直线AB恰好过原点,则A(﹣3,0),B(3,0),N(0,0),
∴ ![]() =(﹣3,0),
=(﹣3,0), ![]() =(5,0),则m=
=(5,0),则m= ![]() ,
,
![]() =(3,0),
=(3,0), ![]() =(﹣1,0),则n=﹣3,
=(﹣1,0),则n=﹣3,
∴m+n= ![]() .
.
若直线AB不过原点,设直线AB:x=ty+2,t≠0,
A(ty1+2,y1),B(ty2+2,y2),N(0,﹣ ![]() ).
).
则 ![]() =(ty1+2,y1+
=(ty1+2,y1+ ![]() ),
), ![]() =(﹣ty1,﹣y1),
=(﹣ty1,﹣y1),
![]() =(ty2+2,y2+
=(ty2+2,y2+ ![]() ),
), ![]() =(﹣ty2,﹣y2),
=(﹣ty2,﹣y2),
由 ![]() ,得y1+
,得y1+ ![]() =m(﹣y1),从而m=
=m(﹣y1),从而m= ![]() ;
;
由 ![]() ,得y2+
,得y2+ ![]() =n(﹣y2),从而n=
=n(﹣y2),从而n= ![]() ;
;
故m+n= ![]() +(
+( ![]() )=
)=  =﹣2﹣
=﹣2﹣ ![]() .
.
联立方程组得: 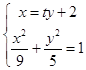 ,整理得(5t2+9)y2+20ty﹣25=0,
,整理得(5t2+9)y2+20ty﹣25=0,
∴y1+y2=﹣ ![]() ,y1y2=
,y1y2= ![]() ,
,
∴m+n=﹣2﹣ ![]() ═
═ ![]() =﹣2﹣
=﹣2﹣ ![]() =
= ![]() .
.
综上所述,m+n= ![]()
【解析】(Ⅰ)求出|ME|+|MF|=6>|EF|=4,判断点M的轨迹是以点E,F为焦点,长轴为6,焦距为4的椭圆,
然后求解方程.(Ⅱ)求出F(2,0),若直线AB恰好过原点,计算m+n的值即可;若直线AB不过原点,设直线AB:x=ty+2,t≠0,求出相关点的坐标与向量,表示出+n,联立直线与椭圆方程的方程组,利用韦达定理,转化求解即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)为R上的可导函数,且对x∈R,均有f(x)>f′(x),则有( )
A.e2016f(﹣2016)<f(0),f(2016)<e2016f(0)
B.e2016f(﹣2016)>f(0),f(2016)>e2016f(0)
C.e2016f(﹣2016)<f(0),f(2016)>e2016f(0)
D.e2016f(﹣2016)>f(0),f(2016)<e2016f(0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)过点(
(a>b>0)过点( ![]() ,1),且焦距为2
,1),且焦距为2 ![]() .
.
(1)求椭圆C的方程;
(2)若直线l:y=k(x+1)(k>﹣2)与椭圆C相交于不同的两点A、B,线段AB的中点M到直线2x+y+t=0的距离为 ![]() ,求t(t>2)的取值范围.
,求t(t>2)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2lnx﹣ax2+3,若存在实数m、n∈[1,5]满足n﹣m≥2时,f(m)=f(n)成立,则实数a的最大值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( ) 
A.4
B.5
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是边长为 3 的菱形,∠ABC=60°,PA⊥平面ABCD,PA=3,F 是棱 PA上的一个动点,E为PD的中点. 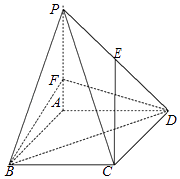
(Ⅰ)若 AF=1,求证:CE∥平面 BDF;
(Ⅱ)若 AF=2,求平面 BDF 与平面 PCD所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知α∈[0,π),在直角坐标系xOy中,直线l1的参数方程为 ![]() (t为参数);在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,直线l2的极坐标方程是ρcos(θ﹣α)=2sin(α+
(t为参数);在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,直线l2的极坐标方程是ρcos(θ﹣α)=2sin(α+ ![]() ).
).
(Ⅰ)求证:l1⊥l2
(Ⅱ)设点A的极坐标为(2, ![]() ),P为直线l1 , l2的交点,求|OP||AP|的最大值.
),P为直线l1 , l2的交点,求|OP||AP|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() (a>b>0)的右焦点为F2(3,0),离心率为e.
(a>b>0)的右焦点为F2(3,0),离心率为e.
(Ⅰ)若 ![]() ,求椭圆的方程;
,求椭圆的方程;
(Ⅱ)设直线y=kx与椭圆相交于A,B两点,M,N分别为线段AF2 , BF2的中点.若坐标原点O在以MN为直径的圆上,且 ![]() ,求k的取值范围.
,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com