
已知函数y=1―2a―2ax+2x2(-1≤x≤1)的最小值为f(a).
(Ⅰ)求f(a)的表达式;
(Ⅱ)当a∈[-2,0]时,求![]() 的值域.
的值域.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源:福建省四地六校联考2010-2011学年高一第三次月考数学试题 题型:044
(1)已知角α终边经过点P(-4,3),求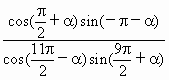 的值?
的值?
(2)已知函数y=a-bcos(x-![]() ),(b>0)在0≤x≤π的最大值为
),(b>0)在0≤x≤π的最大值为![]() ,最小值为-
,最小值为-![]() ,求2a+b的值?
,求2a+b的值?
查看答案和解析>>
科目:高中数学 来源:广东省汕头市澄海中学2010届高三上学期期中考试数学(文)试题 题型:013
定义在R上的函数f(x)满足f(4)=1.![]() (x)为f(x)的导函数,已知函数y=
(x)为f(x)的导函数,已知函数y=![]() (x)的图象如图所示.若两正数a,b满足f(2a+b)<1,则
(x)的图象如图所示.若两正数a,b满足f(2a+b)<1,则![]() 的取值范围是
的取值范围是

(![]() )
)
(-∞,![]() )∪(3,+∞)
)∪(3,+∞)
(![]() ,3)
,3)
(-∞,-3)
查看答案和解析>>
科目:高中数学 来源:2014届安徽省高三上学期第一次月考理科数学试卷(解析版) 题型:选择题
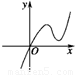
定义在R上的函数f(x)满足f(4)=1,f′(x)为函数f(x)的导函数.已知函数y=f′(x)的图象如图所示,两个正数a、b满足f(2a+b)<1,则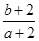 的取值范围是( )
的取值范围是( )
(A)(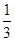 ,
,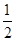 ) (B)(-∞,
) (B)(-∞,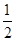 )∪(3,+∞) (C)(
)∪(3,+∞) (C)(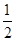 ,3) (D)(-∞,-3)
,3) (D)(-∞,-3)
查看答案和解析>>
科目:高中数学 来源: 题型:
.定义在R上的函数f(x)满足f(4)=1,f′(x)为函数f(x)的导函数.已知函数y=f′(x)的图象如图2所示,两个正数a、b满足f(2a+b)<1,则![]() 的取值范围是( )
的取值范围是( )
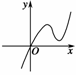
图2
A.(![]() ,
,![]() ) B.(-∞,
) B.(-∞,![]() )∪(3,+∞) C.(
)∪(3,+∞) C.(![]() ,3) D.(-∞,-3)
,3) D.(-∞,-3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com