Question

【题目】已知数列{an}的前n项和为Sn ， 对任意的n∈N* ， 点（n，Sn）恒在函数y= x的图象上．
（1）求数列{an}的通项公式；
（2）记Tn= ，若对于一切的正整数n，总有Tn≤m成立，求实数m的取值范围；
（3）设Kn为数列{bn}的前n项和，其中bn=2an ， 问是否存在正整数n，t，使 成立？若存在，求出正整数n，t；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：由已知，得

当n≥2时，an=Sn﹣Sn﹣1= =3n

当n=1时，a1=S1=3．∴an=3n

（2）

解： ．

当n=1时，Tn+1＞Tn，即T2＞T1；当n=2时，Tn+1=Tn，即T3=T2；

当n≥3时，Tn+1＜Tn，即Tn＜Tn﹣1＜…＜T4＜T3

∴{Tn}中的最大值为 ，

要使Tn≤m对于一切的正整数n恒成立，只需 ∴

解法二：

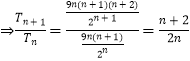
当n=1，2时，Tn+1≥Tn；当n≥3时，n+2＜2nTn+1＜Tn

∴n=1时，T1=9；n=2，3时， n≥4时，Tn＜T3

∴{Tn}中的最大值为 ，

要使Tn≤m对于一切的正整数n恒成立，只需 ∴

（3）

解：

将Kn代入 ，化简得， （﹡）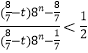

若t=1时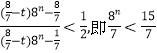， ，显然n=1时成立；

若t＞1时， （﹡）式化简为 不可能成立

综上，存在正整数n=1，t=1使 成立

【解析】（1）利用an=Sn﹣Sn﹣1求解；（2）要使Tn≤m对于一切的正整数n恒成立，只需m≥{Tn}中的最大值即可；（3）求解有关正整数n的不等式．