
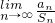 的值;
的值; 和②
和②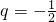 时,分别研究Sn的最值,并说明理由;
时,分别研究Sn的最值,并说明理由;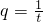 ,t是正整数,t满足不等式|t-63|<62,且对于任意正整数n有9<Sn<12成立,问:这样的数列{an}有几个?
,t是正整数,t满足不等式|t-63|<62,且对于任意正整数n有9<Sn<12成立,问:这样的数列{an}有几个?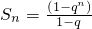 ,则
,则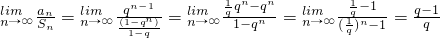 ----(5分)
----(5分) 时,
时,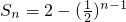 ,所以Sn随n的增大而增大,而S1≤Sn<2,
,所以Sn随n的增大而增大,而S1≤Sn<2,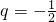 时,
时,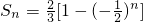
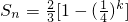 ,所以Sn随k的增大而增大,
,所以Sn随k的增大而增大,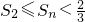 ,即
,即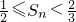
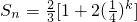 ,所以Sn随k的增大而减小,
,所以Sn随k的增大而减小,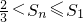 ,即
,即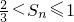
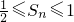 ,Sn有最大值为1,最小值为
,Sn有最大值为1,最小值为 .---(4分)
.---(4分)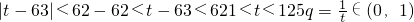 .
.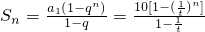 且Sn随着n的增大而增大
且Sn随着n的增大而增大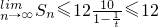 -----------------------(3分)
-----------------------(3分)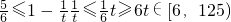 -----------------------------(2分)
-----------------------------(2分)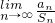 的值;
的值; 时,
时,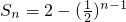 ,所以Sn随n的增大而增大,而S1≤Sn<2,此时Sn有最小值为1,但无最大值当
,所以Sn随n的增大而增大,而S1≤Sn<2,此时Sn有最小值为1,但无最大值当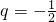 时,
时,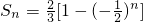 ,分n是偶数,奇数讨论求最大值与最小值
,分n是偶数,奇数讨论求最大值与最小值

 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com