
设函数 ,若关于
,若关于 的方程
的方程 在
在 上恰好有两个相异实根,则实数
上恰好有两个相异实根,则实数 的取值范围为______________.
的取值范围为______________.
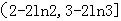
【解析】
试题分析:方程f(x)=x2+x+a可化为x-a+1-ln(1+x)2=0,由于此方程为非基本方程,故求方程的根,可以转化为求对应函数的零点问题,利用导数法我们易构造出满足条件的不等式组,解不等式组即可得到实数a的取值范围.解:若f(x)=x2+x+a,即(1+x)2-ln(1+x)2=x2+x+a,即x-a+1-ln(1+x)2=0,记g(x)=x-a+1-ln(1+x)2,则g'(x)=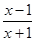 ,令g'(x)>0,得x>1,或x<-1,令g'(x)<0,得-1<x<1,∴g(x)在[0,1]上单调递减,在[1,2]上单调递增;,若方程f(x)=x2+x+a在x∈[0,2]上恰好有两个相异实根,则,g(0)≥0,g(1)<0,g(2)≥0,解得2-2ln2<a≤3-2ln3,故答案为:(2-2ln2,3-2ln3]
,令g'(x)>0,得x>1,或x<-1,令g'(x)<0,得-1<x<1,∴g(x)在[0,1]上单调递减,在[1,2]上单调递增;,若方程f(x)=x2+x+a在x∈[0,2]上恰好有两个相异实根,则,g(0)≥0,g(1)<0,g(2)≥0,解得2-2ln2<a≤3-2ln3,故答案为:(2-2ln2,3-2ln3]
考点:方程的根的分布
点评:本题考查的知识点是方程的根的分布,其中利用方程的根与对应函数之间的关系,将方程f(x)=x2+x+a在x∈[0,2]上恰好有两个相异实根,转化为对应函数在区间∈[0,2]上恰好有两个相异的零点是解答本题的关键.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源:2011-2012学年重庆市高三上学期第十次测试理科数学试卷(解析版) 题型:选择题
设函数 ,若关于
,若关于 的方程
的方程 恰有5个不同的实数解
恰有5个不同的实数解 ,则
,则 等于 (
)
等于 (
)
A.0 B.2lg2 C.3lg2 D.l
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com