已知ABCD-A1B1C1D1为单位正方体,黑白两只蚂蚁从点A出发沿棱向前爬行,每走完一条棱称为“走完一段”,白蚂蚁爬行的路线是AA1→A1D1→…,黑蚂蚁爬行的路线是AB→BB1→…,它们都遵循如下规则:所爬行的第i+2段与第i段所在直线必须是异面直线(其中i是自然数),设黑、白蚂蚁都走完2012段后各停止在正方体的某个顶点处,这时黑、白两只蚂蚁的距离是 .
【答案】
分析:先根据题意,先通过前几步爬行,观察黑蚂蚁与白蚂蚁经过几段后又回到起点,得到每爬6步回到起点,周期为6.再计算黑蚂蚁爬完2012段后实质是到达哪个点以及计算白蚂蚁爬完2012段后实质是到达哪个点,最后计算出它们的距离即可.
解答:
解:由题意,白蚂蚁爬行路线为AA
1→A
1D
1→D
1C
1→C
1C→CB→BA,
即过6段后又回到起点,可以看作以6为周期,
同理,黑蚂蚁也是过6段后又回到起点.
而2012除以6等于335余2
所以黑蚂蚁爬完2012段后回到B
1点,
同理,白蚂蚁爬完2012段后到回到D
1点;
所以它们此时的距离为:B
1D
1=

.
故答案为;
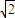
.
点评:本题以一个创新例子为载体,考查归纳推理的能力、空间想象能力、异面直线的定义等相关知识,属于中档题目.

 解:由题意,白蚂蚁爬行路线为AA1→A1D1→D1C1→C1C→CB→BA,
解:由题意,白蚂蚁爬行路线为AA1→A1D1→D1C1→C1C→CB→BA, .
.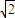 .
.

 如图所示,已知在正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,E为C1C上的点,且CE=1,
如图所示,已知在正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,E为C1C上的点,且CE=1, 如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.