Question

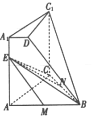
【题目】如图，几何体由一个正三棱柱截去一个三棱锥而得， ， ， ， 平面， 为的中点， 为棱上一点，且平面.

（1）若在棱上，且，证明： 平面；

（2）过作平面的垂线，垂足为，确定的位置（说明作法及理由），并求线段的长.

Answer 1

【答案】(1)证明见解析；(2)答案见解析.

【解析】试题分析：（1）由线面平行的性质定理可证得 .

过作于，连接，则，由此可得，

∴ ，则 .从而可证平面平面.故平面.

（2）在线段上取一点，使， 可知 ，∴，

∴.取的中点，连接，过作于，则平面.

证明：由题意可知，可证平面，∴.又，∴平面.

由射影定理可得.

试题解析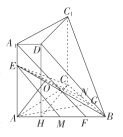：（（1）证明：∵平面， 平面，

平面平面，

∴.

过作于，连接，则，

则，∴，

∴，则.

∵，∴平面平面.

∵平面，∴平面.

（2）解：在线段上取一点，使，则，由（1）知，

∴，∴，

∴.

取的中点，连接，过作于，则平面.

证明如下：由题意可知， 为等边三角形，则，又平面，∴.

∵，∴平面，∴.

又，∴平面.由射影定理可得， ，

又， ，∴.