
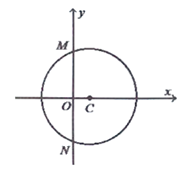
【题目】已知圆心在x轴正半轴上的圆C与直线![]() 相切,与y轴交于M,N两点,且
相切,与y轴交于M,N两点,且![]() .
.
![]() Ⅰ
Ⅰ![]() 求圆C的标准方程;
求圆C的标准方程;
![]() Ⅱ
Ⅱ![]() 过点
过点![]() 的直线l与圆C交于不同的两点D,E,若
的直线l与圆C交于不同的两点D,E,若![]() 时,求直线l的方程;
时,求直线l的方程;
![]() Ⅲ
Ⅲ![]() 已知Q是圆C上任意一点,问:在x轴上是否存在两定点A,B,使得
已知Q是圆C上任意一点,问:在x轴上是否存在两定点A,B,使得![]() ?若存在,求出A,B两点的坐标;若不存在,请说明理由.
?若存在,求出A,B两点的坐标;若不存在,请说明理由.
【答案】(I)![]() ;(II)
;(II)![]() 或
或![]() ;(III)存在
;(III)存在![]() ,
,![]() 或
或![]() ,
,![]() 满足题意.
满足题意.
【解析】
![]() 设圆C的方程为
设圆C的方程为![]() ,利用点C到直线
,利用点C到直线![]() 的距离为
的距离为![]() ,求出a,即可求圆C的标准方程;
,求出a,即可求圆C的标准方程;
![]() Ⅱ
Ⅱ![]() 设直线l的方程为
设直线l的方程为![]() 即
即![]() ,则由题意可知,圆心C到直线l的距离
,则由题意可知,圆心C到直线l的距离![]() ,即可求出k的值,
,即可求出k的值,
![]() Ⅲ
Ⅲ![]() 方法一:假设在x轴上存在两定点
方法一:假设在x轴上存在两定点![]() ,
,![]() ,设
,设![]() 是圆C上任意一点,由题意可得则
是圆C上任意一点,由题意可得则![]() ,即可求出a,b的值,
,即可求出a,b的值,
方法二:设![]() 是圆C上任意一点,由
是圆C上任意一点,由![]() 得
得![]() ,对照圆C的标准方程
,对照圆C的标准方程![]() 即
即![]() ,可得
,可得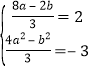 ,解得即可.
,解得即可.
解:![]() Ⅰ
Ⅰ![]() 由题意知圆心
由题意知圆心![]() ,且
,且![]() ,
,
由![]() 知
知![]() 中,
中,![]() ,
,![]() ,则
,则![]() ,
,
于是可设圆C的方程为![]()
又点C到直线![]() 的距离为
的距离为![]() ,
,
所以![]() 或
或![]() 舍
舍![]() ,
,
故圆C的方程为![]() ,
,
![]() Ⅱ
Ⅱ![]() 设直线l的方程为
设直线l的方程为![]() 即
即![]() ,则由题意可知,圆心C到直线l的距离
,则由题意可知,圆心C到直线l的距离![]() ,
,
故![]() ,解得
,解得![]() ,
,
又当![]() 时满足题意,
时满足题意,
因此所求的直线方程为![]() 或
或![]() ,
,
![]() Ⅲ
Ⅲ![]() 方法一:假设在x轴上存在两定点
方法一:假设在x轴上存在两定点![]() ,
,![]() ,设
,设![]() 是圆C上任意一点,则
是圆C上任意一点,则![]() 即
即![]() ,
,
则![]() ,
,
令![]() ,
,
解得![]() 或
或![]() ,
,
因此存在![]() ,
,![]() ,
,![]() 或
或![]() ,
,![]() 满足题意,
满足题意,
方法二:设![]() 是圆C上任意一点,
是圆C上任意一点,
由![]() 得
得![]() ,
,
化简可得![]() ,
,
对照圆C的标准方程![]() 即
即![]() ,
,
可得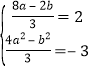 ,
,
解得解得![]() 或
或![]() ,
,
因此存在![]() ,
,![]() 或
或![]() ,
,![]() 满足题意.
满足题意.


科目:高中数学 来源: 题型:
【题目】给定函数![]() ,若对于定义域中的任意
,若对于定义域中的任意![]() ,都有
,都有![]()
![]() 恒成立,则称函数
恒成立,则称函数![]() 为“爬坡函数”.
为“爬坡函数”.
(Ⅰ)证明:函数![]() 是“爬坡函数”;
是“爬坡函数”;
(Ⅱ)若函数![]() 是“爬坡函数”,求实数
是“爬坡函数”,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若对任意的实数![]() ,函数
,函数![]() 都不是“爬坡函数”,求实数
都不是“爬坡函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)满足xf′(x)﹣f(x)>0,当0<m<n<1时,下面选项中最大的一项是( )
A.![]()
B.logmn?f(lognm)
C.![]()
D.lognm?f(logmn)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划投资A、B两种金融产品,根据市场调查与预测,A产品的利润与投资量成正比例,其关系如图1,B产品的利润与投资量的算术平方根成正比例,其关系如图2(注:利润与投资量的单位:万元).
(1)分别将A、B两产品的利润表示为投资量的函数关系式;
(2)该公司已有10万元资金,并全部投入A、B两种产品中,问:怎样分配这10万元投资,才能使公司获得最大利润?其最大利润为多少万元?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了对教师教学水平和教师管理水平进行评价,从该校学生中选出300人进行统计.其中对教师教学水平给出好评的学生人数为总数的60%,对教师管理水平给出好评的学生人数为总数的75%,其中对教师教学水平和教师管理水平都给出好评的有120人.
(1)填写教师教学水平和教师管理水平评价的2×2列联表:
对教师管理水平好评 | 对教师管理水平不满意 | 合计 | |
对教师教学水平好评 | |||
对教师教学水平不满意 | |||
合计 |
问:是否可以在犯错误概率不超过0.1%的前提下,认为教师教学水平好评与教师管理水平好评有关、
(2)若将频率视为概率,有4人参与了此次评价,设对教师教学水平和教师管理水平全好评的人数为随机变量X;
①求对教师教学水平和教师管理水平全好评的人数X的分布列(概率用组合数算式表示);
②求X的数学期望和方差.
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
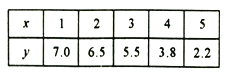
【题目】为了了解某地区某种农产品的年产量![]() (单位:吨)对价格
(单位:吨)对价格![]() (单位:千元/吨)和利润
(单位:千元/吨)和利润![]() 的影响,对近五年该农产品的年产量和价格统计如下表:
的影响,对近五年该农产品的年产量和价格统计如下表:
参考公式: 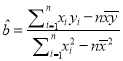 ,
, ![]() .
.
根据参考公式,以求得![]()
(1)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润![]() 取到最大值?(保留两位小数)
取到最大值?(保留两位小数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com