
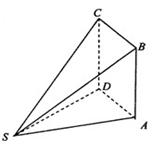
如图,多面体ABCDS中,面ABCD为矩形,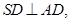 且
且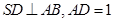 ,
,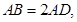
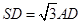 。(I)求多面体ABCDS的体积;(II)求AD与SB所成角的余弦值;(III)求二面角A—SB—D的余弦值。
。(I)求多面体ABCDS的体积;(II)求AD与SB所成角的余弦值;(III)求二面角A—SB—D的余弦值。
(1)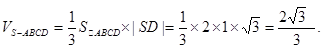 (2)
(2)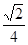 ;(3)
;(3)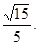
【解析】本试题主要是考查同学们运用点线面的位置关系,求解异面直线所成的角,以及二面角的求解问题。培养了同学们的空间想象能力和逻辑推理能力和计算能力的运用。
(1)因为多面体ABCDS的体积即四棱锥S—ABCD的体积。利用棱锥的体积公式求解得到。
(2)分析; 要求AD与SB所成的角,即求BC与SB所成的角,那么利用平移法得到角,解三角形得到结论。
(3)利用三垂线定理得到二面角,然后借助于三角形的知识求解得到。
解:(I)多面体ABCDS的体积即四棱锥S—ABCD的体积。
所以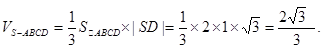
II)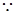 矩形ABCD,
矩形ABCD,
|
 AD//BC,即BC=a,
AD//BC,即BC=a,
 要求AD与SB所成的角,即求BC与SB所成的角在
要求AD与SB所成的角,即求BC与SB所成的角在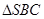 中,由(1)知
中,由(1)知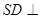 面ABCD。
面ABCD。
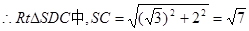
 CD是CS在面ABCD内的射影,且
CD是CS在面ABCD内的射影,且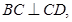
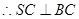
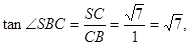
 BC与SB所成的角的余弦为
BC与SB所成的角的余弦为
从而SB与AD的成的角的余弦为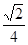
(III)
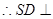 面ABCD。
面ABCD。
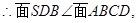 BD为面SDB与面ABCD的交线。
BD为面SDB与面ABCD的交线。

 SDB
SDB
 于F,连接EF从而得:
于F,连接EF从而得: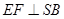
 为二面角A—SB—D的平面角
为二面角A—SB—D的平面角
在矩形ABCD中,对角线
 中,
中,
由(2)知在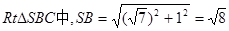
而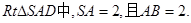

 为等腰直角三角形且
为等腰直角三角形且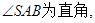
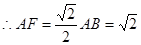
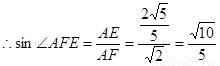 ,
,
所以所求的二面角的余弦为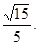


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:

| AK |
| AE |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年东北师大附中、哈师大附中、辽宁实验中学高三第二次模拟考试数学理卷 题型:解答题
((本小题满分12分)
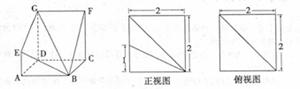
如图,多面体ABCD—EFG中,底面ABCD为正方形,GD//FC//AE,AE⊥平面ABCD,其正视图、俯视图如下:

(I)求证:平面AEF⊥平面BDG;
(II)若存在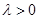 使得
使得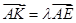 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为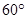 ,求
,求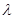 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2010-2011年浙江省高二下学期期中考试理数试题 题型:选择题
((本小题满分12分)
如图,多面体ABCD—EFG中,底面ABCD为正方形,GD//FC//AE,AE⊥平面ABCD,其正视图、俯视图如下:
(I)求证:平面AEF⊥平面BDG;
(II)若存在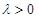 使得
使得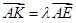 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为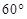 ,求
,求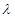 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2010-2011年东北师大附中、哈师大附中、辽宁实验中学高二第二次考试数学理卷 题型:解答题
(本小题满分12分)
如图,多面体ABCD—EFG中,底面ABCD为正方形,GD//FC//AE,AE⊥平面ABCD,其正视图、俯视图如下:
(I)求证:平面AEF⊥平面BDG;

(II)若存在 使得
使得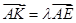 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为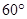 ,求
,求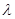 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:模拟题 题型:解答题
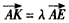 ,KF与平面ABG所成角为30°,求λ的值。
,KF与平面ABG所成角为30°,求λ的值。 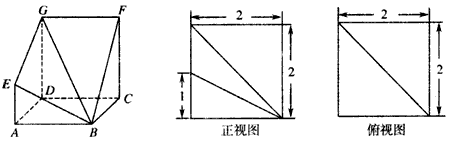
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com