练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图所示，设S为平面上以点A(4，1)，B(-1，-6)，C(-3，2)为顶点的三角形区域(三角形内部及边界)，试求当点(x，y)在区域S上变动时t=4x-3y的最大值和最小值．

     

    答案：
    解析：

    解：平行线t=4x-3y过点A时t=13，过点B时t=14，过点C时t=-18，因而t的最大值14，最小值为-18．

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

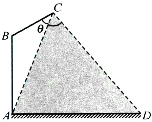    在路边安装路灯，灯柱AB与地面垂直，灯杆BC与灯柱AB所在平面与道路垂直，且∠ABC=120°，路灯C采用锥形灯罩，射出的光线如图中阴影部分所示，已知∠ACD=60°，路宽AD=24m．设灯柱高AB=h（m），∠ACB=θ（30°≤θ≤45°）．
    （1）求灯柱的高h（用θ表示）；
    （2）若灯杆BC与灯柱AB所用材料相同，记此用料长度和为S，求S关于θ的函数表达式，并求出S的最小值．

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

    如图所示，设S为平面上以点A(4，1)，B(-1，-6)，C(-3，2)为顶点的三角形区域(三角形内部及边界)，试求当点(x，y)在区域S上变动时t=4x-3y的最大值和最小值．

     

    查看答案和解析>>

    科目：高中数学 来源：天骄之路中学系列　读想用　高二数学(上) 题型：044

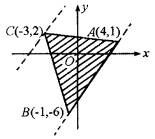
    如图所示，设S为平面上以点A(4，1)，B(－1，－6)，C(－3，2)为顶点的三角形区域(三角形内部及边界)，试求当点(x，y)在区域S上变动时t＝4x－3y的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    (2007全国Ⅱ，19)如图所示，在四棱锥S－ABCD中，底面ABCD为正方形，侧棱SD⊥底面ABCD，E、F分别是AB、SC的中点．

    (1)证明：EF∥平面SAD；

    (2)设SD=2DC，求二面角A－EF－D的大小．

    查看答案和解析>>

    同步练习册答案