二次函数f(x)满足f(x+1)-f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)若不等式f(x)>2x+m在区间,[-1,1]上恒成立,求实数m的取值范围.
解:(1)由f(0)=1,可设f(x)=ax
2+bx+1(a≠0)
∵f(x+1)-f(x)=2x,
∴a(x+1)
2+b(x+1)+1-(ax
2+bx+1)=2ax+a+b
由题意得,
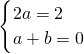
,解得
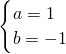
;
故f(x)=x
2-x+1
(2)由题意得,x
2-x+1>2x+m
即x
2-3x+1>m 对x∈[-1,1]恒成立,
令g(x)=x
2-3x+1,又g(x)在[-1,1]上递减,故g(x)
min=g(1)=-1
故m<-1
分析:(1)由f(0)=1,可设f(x)=ax
2+bx+1(a≠0),代入f(x+1)-f(x)=2x,根据系数对应相等可求a,b进而可求f(x)
(2)由题意得,x
2-x+1>2x+m,即x
2-3x+1>m 对x∈[-1,1]恒成立,令g(x)=x
2-3x+1,根据g(x)在[-1,1]上的单调性可求g(x)
min,可求m的范围
点评:本题主要考查了利用待定系数法求解二次函数的函数解析式,及函数的恒成立与函数的最值求解的相互转化,主要单调性在函数的最值求解中的应用.

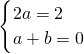 ,解得
,解得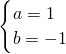 ;
;
