
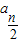 .
. ,(n∈N*),由此得该数列的前6项.
,(n∈N*),由此得该数列的前6项.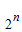 )=[1+3+5+7+…+(2n-1)]+[1+3+5+7+…+(2n-1-1)]+[1+3+5+7+…+(2n-2-1)]+…+(1+3)+1,根据1+3+5+7+…+(2n-1)=4n-1,可得 Tn =4n-1+4n-2+4n-3+…+41+4+1,根据等比数列前n项和公式求得结果.
)=[1+3+5+7+…+(2n-1)]+[1+3+5+7+…+(2n-1-1)]+[1+3+5+7+…+(2n-2-1)]+…+(1+3)+1,根据1+3+5+7+…+(2n-1)=4n-1,可得 Tn =4n-1+4n-2+4n-3+…+41+4+1,根据等比数列前n项和公式求得结果. ,(n∈N*)
,(n∈N*)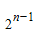 )
)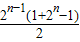 =(2n-1)2=4n-1,
=(2n-1)2=4n-1,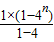 +1=
+1=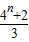 .
.

科目:高中数学 来源: 题型:
| n | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(07年西城区抽样理)(14分) 对于数列![]() ,定义数列
,定义数列![]() 为
为![]() 的“差数列”.
的“差数列”.
(I)若![]() 的“差数列”是一个公差不为零的等差数列,试写出
的“差数列”是一个公差不为零的等差数列,试写出![]() 的一个通项公式;
的一个通项公式;
(II)若![]()
![]() 的“差数列”的通项为
的“差数列”的通项为![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() ;
;
(III)对于(II)中的数列![]() ,若数列
,若数列![]() 满足
满足![]()
求:①数列![]() 的通项公式;②当数列
的通项公式;②当数列![]() 前n项的积最大时n的值.
前n项的积最大时n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(07年上海卷理)(18分)
若有穷数列![]() (
(![]() 是正整数),满足
是正整数),满足![]() 即
即![]() (
(![]() 是正整数,且
是正整数,且![]() ),就称该数列为“对称数列”。
),就称该数列为“对称数列”。
(1)已知数列![]() 是项数为7的对称数列,且
是项数为7的对称数列,且![]() 成等差数列,
成等差数列,![]() ,试写出
,试写出![]() 的每一项
的每一项
(2)已知![]() 是项数为
是项数为![]() 的对称数列,且
的对称数列,且![]() 构成首项为50,公差为
构成首项为50,公差为![]() 的等差数列,数列
的等差数列,数列![]() 的前
的前![]() 项和为
项和为![]() ,则当
,则当![]() 为何值时,
为何值时,![]() 取到最大值?最大值为多少?
取到最大值?最大值为多少?
(3)对于给定的正整数![]() ,试写出所有项数不超过
,试写出所有项数不超过![]() 的对称数列,使得
的对称数列,使得![]() 成为数列中的连续项;当
成为数列中的连续项;当![]() 时,试求其中一个数列的前2008项和
时,试求其中一个数列的前2008项和![]()
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市长宁区高三教学质量测试理科数学 题型:填空题
(理)把正整数排列成如图甲三角形数阵,然后擦去第偶数行中的奇数和第奇数行中的偶数,得到如图乙的三角形数阵,再把图乙中的数按从小到大的顺序排成一列,得到一个数列 ,若
,若 ,则
,则 __________.
__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com