
【题目】已知函数![]() ,求:
,求:
(1)函数![]() 的图象在点(0,-2)处的切线方程;
的图象在点(0,-2)处的切线方程;
(2)![]() 的单调递减区间.
的单调递减区间.
【答案】(1)9x﹣y﹣2=0.(2)f(x)的单调递减区间为(﹣∞,﹣1),(3,+∞).
【解析】
(1)求出f′(x)=﹣3x2+6x+9,f′(0)=9,f(0)=﹣2,由此利用导数的几何意义能求出函数y=f(x)的图象在点(0,f(0))处的切线方程.
(2)由f′(x)=﹣3x2+6x+9<0,能求出f(x)的单调递减区间.
(1)∵f(x)=﹣x3+3x2+9x﹣2,
∴f′(x)=﹣3x2+6x+9,
f′(0)=9,f(0)=﹣2,
∴函数y=f(x)的图象在点(0,f(0))处的切线方程为:
y+2=9x,即9x﹣y﹣2=0.
(2)∵f(x)=﹣x3+3x2+9x﹣2,
∴f′(x)=﹣3x2+6x+9,
由f′(x)=﹣3x2+6x+9<0,
解得x<﹣1或x>3.
∴f(x)的单调递减区间为(﹣∞,﹣1),(3,+∞).


科目:高中数学 来源: 题型:
【题目】设数列{an}的各项都为正数,其前n项和为Sn,已知对任意n∈N*,Sn是![]() 和an的等差中项.
和an的等差中项.
(1)证明:数列{an}为等差数列;
(2)若bn=-n+5,求{an·bn}的最大项的值并求出取最大值时n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某住宅小区为了使居民有一个优雅舒适的生活环境,计划建一个八边形的休闲小区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的面积为200平方米的十字型地域.现计划在正方形MNPQ上建花坛,造价为4200元/平方米,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元/平方米,再在四个空角上铺草坪,造价为80元/平方米.
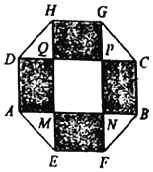
(1)设总造价为S元,AD的边长为x米,DQ的边长为y米,试建立S关于x的函数关系式;
(2)计划至少要投入多少元,才能建造这个休闲小区.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:已知函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,若
,若![]() 恒成立,则称函数
恒成立,则称函数![]() 在
在![]() 上具有“
上具有“![]() ”性质.
”性质.
(![]() )判断函数
)判断函数![]() 在
在![]() 上是否具有“
上是否具有“![]() ”性质?说明理由.
”性质?说明理由.
(![]() )若
)若![]() 在
在![]() 上具有“
上具有“![]() ”性质,求
”性质,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,下列说法错误的是( )
,下列说法错误的是( )
A. 若![]() 有最大值,则
有最大值,则![]() 也有最大值
也有最大值
B. 若![]() 有最大值,则
有最大值,则![]() 也有最大值
也有最大值
C. 若数列![]() 不单调,则数列
不单调,则数列![]() 也不单调
也不单调
D. 若数列![]() 不单调,则数列
不单调,则数列![]() 也不单调
也不单调
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在高为6的等腰梯形![]() 中,
中, ![]() ,且
,且![]() ,
, ![]() ,将它沿对称轴
,将它沿对称轴![]() 折起,使平面
折起,使平面![]() 平面
平面![]() .如图2,点
.如图2,点![]() 为
为![]() 中点,点
中点,点![]() 在线段
在线段![]() 上(不同于
上(不同于![]() ,
, ![]() 两点),连接
两点),连接![]() 并延长至点
并延长至点![]() ,使
,使![]() .
.
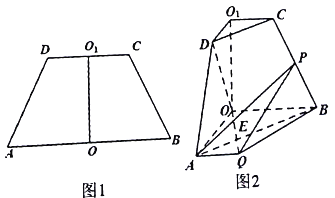
(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 上一动点,
上一动点,![]() 为坐标原点,则线段
为坐标原点,则线段![]() 中点
中点![]() 的轨迹方程为_______.
的轨迹方程为_______.
【答案】![]()
【解析】
设出![]() 点的坐标,由此得到
点的坐标,由此得到![]() 点的坐标,将
点的坐标,将![]() 点坐标代入椭圆方程,化简后可得
点坐标代入椭圆方程,化简后可得![]() 点的轨迹方程.
点的轨迹方程.
设![]() ,由于
,由于![]() 是
是![]() 中点,故
中点,故![]() ,代入椭圆方程得
,代入椭圆方程得![]() ,化简得
,化简得![]() .即
.即![]() 点的轨迹方程为
点的轨迹方程为![]() .
.
【点睛】
本小题主要考查代入法求动点的轨迹方程,考查中点坐标,属于基础题.
【题型】填空题
【结束】
15
【题目】设![]() 是双曲线
是双曲线![]() :
:![]() 的右焦点,
的右焦点,![]() 是
是![]() 左支上的点,已知
左支上的点,已知![]() ,则
,则![]() 周长的最小值是_______.
周长的最小值是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com