
【题目】设区间![]() ,定义在
,定义在![]() 上的函数
上的函数![]() (
(![]() ),集合
),集合![]() .
.
(1)若![]() ,求集合
,求集合![]() ;
;
(2)设常数![]() .
.
① 讨论![]() 的单调性;
的单调性;
② 若![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() (2)①见解析;②见证明
(2)①见解析;②见证明
【解析】
(1)把b![]() 代入函数解析式,求出导函数,由f′(x)
代入函数解析式,求出导函数,由f′(x)![]() 0,可知f(x)在[﹣3,3]上为增函数,求出函数的最小值,由最小值大于0求得a的取值范围;
0,可知f(x)在[﹣3,3]上为增函数,求出函数的最小值,由最小值大于0求得a的取值范围;
(2)①求出函数的导函数,解得导函数的零点,然后根据![]() 与3的关系分类求得函数的单调区间;
与3的关系分类求得函数的单调区间;
②当b<﹣1时,由①可知,当0<a![]() 时,求得函数的最小值小于0,得到矛盾,故此时实数a不存在;当a
时,求得函数的最小值小于0,得到矛盾,故此时实数a不存在;当a![]() 时,由①可得f(x)min={f(﹣3),f(
时,由①可得f(x)min={f(﹣3),f(![]() )},得到f(﹣3)<0,这与x∈D,f(x)≥0恒成立矛盾,故此时实数a不存在;若f(﹣3)>0,证明f(
)},得到f(﹣3)<0,这与x∈D,f(x)≥0恒成立矛盾,故此时实数a不存在;若f(﹣3)>0,证明f(![]() )<0,这与x∈D,f(x)≥0恒成立矛盾,故此时实数a不存在.
)<0,这与x∈D,f(x)≥0恒成立矛盾,故此时实数a不存在.
(1)当![]() 时,
时,![]() ,则
,则![]() .
.
由![]() 可知
可知![]() 恒成立,故函数
恒成立,故函数![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,解得
,解得![]() ,
,
所以集合![]()
(2)① 由![]() 得
得![]() ,
,
因为![]() ,则由
,则由![]() ,得
,得![]() .
.
在![]() 上列表如下:
上列表如下:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
(ⅰ)当![]() ,即
,即![]() 时,
时,
则![]() ,所以
,所以![]() 在
在![]() 上单调递减;
上单调递减;
(ⅱ)当![]() ,即
,即![]() 时,此时
时,此时![]() ,
,
![]() 在
在![]() 和
和![]() 上单调递增;在
上单调递增;在![]() 上单调递减.
上单调递减.
综上,当![]() 时,
时,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在![]() ,
,![]() 上单调递增;
上单调递增;
在![]() 上单调递减
上单调递减
②(方法一)当![]() 时,由①可知,
时,由①可知,
(ⅰ)当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,
,
这与![]() 恒成立矛盾,故此时实数
恒成立矛盾,故此时实数![]() 不存在;
不存在;
(ⅱ)当![]() 时,
时,![]() 在
在![]() ,
,![]() 上单调递增;
上单调递增;
在![]() 上单调递减,
上单调递减,
所以![]() .
.
若![]() ,这与
,这与![]() 恒成立矛盾,
恒成立矛盾,
故此时实数![]() 不存在;
不存在;
若![]() ,此时
,此时![]() ,
,
又![]() ,则
,则![]() ,
,
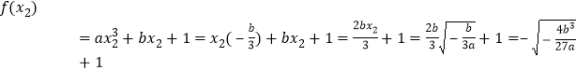 .
.
下面证明![]() ,也即证:
,也即证:![]() .
.
因为![]() ,且
,且![]() ,则
,则![]() ,
,
下证:![]() .
.
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,即
,即![]() .
.
这与![]() 恒成立矛盾,故此时实数
恒成立矛盾,故此时实数![]() 不存在.
不存在.
综上所述,![]() .
.
(方法二)(ⅰ)当![]() 时,
时,![]() 成立;
成立;
(ⅱ)当![]() 时,由题意可知
时,由题意可知![]() 恒成立,则
恒成立,则![]() ,
,
设![]() ,则
,则![]() ,
,
令![]() ,解得
,解得![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() ,所以
,所以![]() ;
;
(ⅲ)当![]() 时,由题意可知
时,由题意可知![]() 恒成立,则
恒成立,则![]() .
.
设![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,
,
所以![]() .
.
若![]() ,则存在实数
,则存在实数![]() 满足
满足![]() ,
,
则![]() 成立,即
成立,即![]() ,
,
也即![]() 成立,
成立,
则![]() ,这与
,这与![]() 矛盾,所以
矛盾,所以![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》卷第五《商功》中有记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”现有一个刍甍,如图,四边形![]() 为正方形,四边形
为正方形,四边形![]() 、
、![]() 为两个全等的等腰梯形,
为两个全等的等腰梯形,![]() ,
,![]() ,若这个刍甍的体积为
,若这个刍甍的体积为![]() ,则
,则![]() 的长为( )
的长为( )
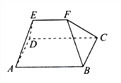
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度![]() (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度![]() (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当![]() 时,
时,![]() 的值为2千克/年;当
的值为2千克/年;当![]() 时,
时,![]() 是
是![]() 的一次函数;当
的一次函数;当![]() 时,因缺氧等原因,
时,因缺氧等原因,![]() 的值为0千克/年.
的值为0千克/年.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(2)当养殖密度![]() 为多少时,鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
为多少时,鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
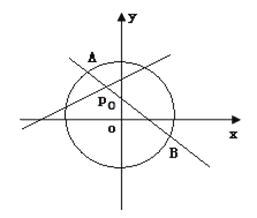
【题目】已知圆O:x2+y2=8内有一点P0(﹣1,2),AB为过点P0且倾斜角为α的弦.
(1)当α=135°时,求弦AB的长;
(2)当弦AB被P0平分时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像关于直线
的图像关于直线![]() 对称,且
对称,且![]() .
.
(1)求![]() 的表达式;
的表达式;
(2)若将![]() 图像上各点的横坐标变为原来的
图像上各点的横坐标变为原来的![]() ,再将所得图像向右平移
,再将所得图像向右平移![]() 个单位,得到
个单位,得到![]() 的图像,且关于
的图像,且关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有且只有一个实数解,求实数
上有且只有一个实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第二届中国国际进口博览会于2019年11月5日至10日在上海国家会展中心举行,来自151个国家和地区的3617家企业参展,规模和品质均超过首届.更多新产品、新技术、新服务“全球首发,中国首展”,专(业)精(品)尖(端)特(色)产品精华荟萃.某跨国公司带来了高端空调模型参展,通过展会调研,中国甲企业计划在2020年与该跨国公司合资生产此款空调.生产此款空调预计全年需投入固定成本260万元,每生产x千台空调,需另投入资金![]() 万元,且
万元,且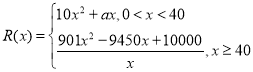 .经测算生产10千台空调需另投入的资金为4000万元.由调研知,每台空调售价为0.9万元时,当年内生产的空调当年能全部销售完.
.经测算生产10千台空调需另投入的资金为4000万元.由调研知,每台空调售价为0.9万元时,当年内生产的空调当年能全部销售完.
(1)求2020年的企业年利润![]() (万元)关于年产量x(千台)的函数关系式;
(万元)关于年产量x(千台)的函数关系式;
(2)2020年产量为多少(千台)时,企业所获年利润最大?最大年利润是多少?注:利润=销售额–成本
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为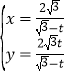 (
(![]() 为参数,且
为参数,且![]() ),以坐标原点为极点,
),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 的参数方程化为普通方程,并将曲线
的参数方程化为普通方程,并将曲线![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求曲线![]() 与曲线
与曲线![]() 交点的极坐标
交点的极坐标![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com