
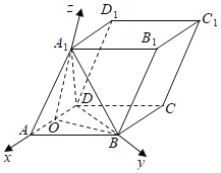
【题目】如图,在平行六面体![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
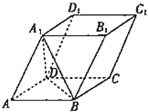
(1)证明:![]() .
.
(2)若平面![]() 平面
平面![]() ,且
,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,推导出
,推导出![]() ,
,![]() ,从而
,从而![]() 平面
平面![]() ,由此能证明
,由此能证明![]() .
.
(2)推导出![]() 平面
平面![]() ,以
,以![]() 为原点,分别以
为原点,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,利用向量法能求出二面角
,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
解:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,
,
又![]() ,四边形
,四边形![]() 是平行四边形,
是平行四边形,![]() ,
,
∴![]() 是等边三角形,∴
是等边三角形,∴![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.
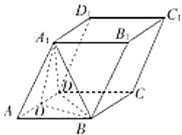
(2)∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
又![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
![]()
∴![]() ,
,![]() ,
,![]() 两两垂直,
两两垂直,
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 、
、![]() 、
、![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立如图所示空间直角坐标系
轴,建立如图所示空间直角坐标系![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
易知平面![]() 的一个法向量为
的一个法向量为![]() ,
,
![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则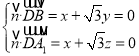 ,取
,取![]() ,得
,得![]() ,
,
即平面![]() 的一个法向量为
的一个法向量为![]() ,
,
![]() ,
,![]() ,
,![]()
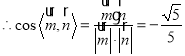 ,
,
由图易知二面角![]() 为锐二面角,
为锐二面角,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,过
,过![]() 的焦点且垂直于
的焦点且垂直于![]() 轴的直线被
轴的直线被![]() 截得的弦长为
截得的弦长为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)经过右焦点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴相交于点
轴相交于点![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() (a>b>0)的左、右焦点分别为
(a>b>0)的左、右焦点分别为![]() ,
,![]() . 已知
. 已知![]() 和
和![]() 都在椭圆上,其中
都在椭圆上,其中![]() 为椭圆的离心率.
为椭圆的离心率.
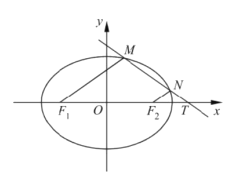
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过![]() 作斜率为
作斜率为![]()
![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(
两点(![]() 点在
点在![]() 点的左侧),且
点的左侧),且![]() . 若
. 若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现将“□”和“○”按照如下规律从左到右进行排列:若每一个“□”或“○”占1个位置,即上述图形中,第1位是“□”,第4位是“○”,第7位是 “□”,则在第2017位之前(不含第2017位),“○”的个数为( )
□,○,□,○,○,○,□,○,○,○,○,○,□,○,○,○,○,○,○,○![]()
A.1970B.1971C.1972D.1973
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的两个焦点分别为
的两个焦点分别为![]() ,点M(1,0)与椭圆短轴的两个端点的连线相互垂直.
,点M(1,0)与椭圆短轴的两个端点的连线相互垂直.
(1)求椭圆C的方程;
(2)过点M(1,0)的直线与椭圆C相交于A、B两点,设点N(3,2),记直线AN、BN的斜率分别为k1、k2,求证:k1+k2为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋子中有5个大小相同的球,其中3个白球与2个黑球,现从袋中任意取出一个球,取出后不放回,然后再从袋中任意取出一个球,则第一次为白球、第二次为黑球的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
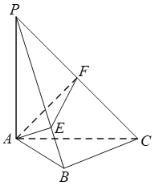
【题目】在《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑.如图,在鳖臑![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,过点
,过点![]() 分别作
分别作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连结
,连结![]() ,当
,当![]() 的面积最大时,
的面积最大时,![]() __________.
__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com