[题目]学校艺术节对同一类的...四项参赛作品.只评一项一等奖.在评奖揭晓前.甲.乙.丙.丁四位同学对这四项参赛作品预测如下:甲说:“是或作品获得一等奖 ,乙说:“作品获得一等奖 ,丙说:“.两项作品未获得一等奖 ,丁说:“是作品获得一等奖 .若这四位同学中只有两位说的话是对的.则获得一等奖的作品是．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】学校艺术节对同一类的，，，四项参赛作品，只评一项一等奖，在评奖揭晓前，甲、乙、丙、丁四位同学对这四项参赛作品预测如下：

甲说：“是或作品获得一等奖”；

乙说：“作品获得一等奖”；

丙说：“，两项作品未获得一等奖”；

丁说：“是作品获得一等奖”.

若这四位同学中只有两位说的话是对的，则获得一等奖的作品是__________．

【答案】B

【解析】若A为一等奖，则甲，丙，丁的说法均错误，故不满足题意，

若B为一等奖，则乙，丙说法正确，甲，丁的说法错误，故满足题意，

若C为一等奖，则甲，丙，丁的说法均正确，故不满足题意，

若D为一等奖，则只有甲的说法正确，故不合题意，

故若这四位同学中只有两位说的话是对的，则获得一等奖的作品是B

故答案为：B

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图,已知一个八面体的各条棱长为1,四边形ABCD为正方形,下列说法

①该八面体的体积为;

②该八面体的外接球的表面积为;

③E到平面ADF的距离为;

④EC与BF所成角为60°;

其中不正确的个数为

A. 0 B. 1 C. 2 D. 3

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某学校要对如图所示的5个区域进行绿化（种花），现有4种不同颜色的花供选择，要求相邻区域不能种同一种颜色的花，则共有___________种不同的种花方法.

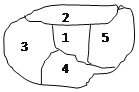
查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知△ABC的内角A，B，C满足sin2A+sin（A﹣B+C）=sin（C﹣A﹣B）+ ，面积S满足1≤S≤2，记a，b，c分别为A，B，C所对的边，在下列不等式一定成立的是（）
A.bc（b+c）＞8
B.ab（a+b）＞16
C.6≤abc≤12
D.12≤abc≤24

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，四棱锥P﹣ABCD，底面是以O为中心的菱形，PO⊥底面ABCD，AB=2，∠BAD= ，M为BC上的一点，且BM= ，MP⊥AP．

（1）求PO的长；
（2）求二面角A﹣PM﹣C的正弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某几何体的三视图（单位：cm）如图所示，则此几何体的表面积是（）

A.90cm2
B.129cm2
C.132cm2
D.138cm2

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】记max{x，y}= ，min{x，y}= ，设，为平面向量，则（）
A.min{| + |，| ﹣ |}≤min{| |，| |}
B.min{| + |，| ﹣ |}≥min{| |，| |}
C.max{| + |2 ， | ﹣ |2}≤| |2+| |2
D.max{| + |2 ， | ﹣ |2}≥| |2+| |2