
【题目】已知函数![]()
![]()
(1)求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)证明:![]() .
.
【答案】(1)![]() (2)详见解析
(2)详见解析
【解析】
试题分析:(1)利用导数几何意义得:曲线![]() 在
在![]() 处的切线斜率等于该点处导数值,k=f′(1)=e,而f(1)=2,利用点斜式得切线方程为
处的切线斜率等于该点处导数值,k=f′(1)=e,而f(1)=2,利用点斜式得切线方程为![]() (2)先调整所证不等式:
(2)先调整所证不等式:![]() 等价于
等价于![]() ,再利用导数分别研究左右函数最值:设函数g(x)=xln x,g(x)在(0,+∞)上的最小值为g
,再利用导数分别研究左右函数最值:设函数g(x)=xln x,g(x)在(0,+∞)上的最小值为g![]() =-
=-![]() ;设函数h(x)=xe-x-
;设函数h(x)=xe-x-![]() ,则h(x)在(0,+∞)上的最大值为h(1)=-
,则h(x)在(0,+∞)上的最大值为h(1)=-![]() .但两个函数取最值时的自变量不同,因此等于号取不到,从而得证.
.但两个函数取最值时的自变量不同,因此等于号取不到,从而得证.
试题解析:解:(1)函数f(x)的定义域为(0,+∞),
![]()
由题意可得f(1)=2,f′(1)=e,故曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ;
;
(2)证明:由(1)知,f(x)=exln x+![]() ex-1,
ex-1,
从而![]() 等价于
等价于![]() .
.
设函数g(x)=xln x,
则g′(x)=1+ln x,
所以当x∈![]() 时,g′(x)<0;
时,g′(x)<0;
当x∈![]() 时,g′(x)>0.
时,g′(x)>0.
故g(x)在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,从而g(x)在(0,+∞)上的最小值为
上单调递增,从而g(x)在(0,+∞)上的最小值为
g![]() =-
=-![]() .
.
设函数h(x)=xe-x-![]() ,则h′(x)=e-x(1-x).
,则h′(x)=e-x(1-x).
所以当x∈(0,1)时,h′(x)>0;
当x∈(1,+∞)时,h′(x)<0.
故h(x)在(0,1)上单调递增,在(1,+∞)上单调递减,从而h(x)在(0,+∞)上的最大值为
h(1)=-![]() .
.
因为gmin(x)=g![]() =h(1)=hmax(x),
=h(1)=hmax(x),
所以当x>0时,g(x)>h(x),即f(x)>1.


科目:高中数学 来源: 题型:
【题目】调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图,则下列结论中不一定正确的是( )

A. 互联网行业从业人员中90后占一半以上
B. 互联网行业中从事技术岗位的人数超过总人数的![]()
C. 互联网行业中从事运营岗位的人数90后比80前多
D. 互联网行业中从事运营岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校统计了本校高一年级学生期中考试的数学成绩,其数学成绩(满分150分)均在![]() 内,将这些成绩分成
内,将这些成绩分成![]() 5组,得到如图所示的频率分布直方图.
5组,得到如图所示的频率分布直方图.
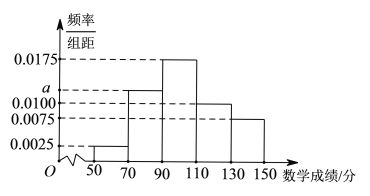
(1)求a的值;
(2)求该校高一年级学生期中考试的数学成绩的中位数(结果保留一位小数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了反映国民经济各行业对仓储物流业务的需求变化情况,以及重要商品库存变化的动向,中国物流与采购联合会和中储发展股份有限公司通过联合调查,制定了中国仓储指数.如图所示的折线图是2016年1月至2017年12月的中国仓储指数走势情况.

根据该折线图,下列结论正确的是
A. 2016年各月的仓储指数最大值是在3月份
B. 2017年1月至12月的仓储指数的中位数为54%
C. 2017年1月至4月的仓储指数比2016年同期波动性更大
D. 2017年11月的仓储指数较上月有所回落,显示出仓储业务活动仍然较为活跃,经济运行稳中向好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,以极轴为
,以极点为原点,以极轴为![]() 轴的正半轴,取相同的单位长度,建立平面直角坐标系,直线
轴的正半轴,取相同的单位长度,建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为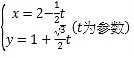 .
.
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,曲线
,曲线![]() 上任一点为
上任一点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() 、
、![]() ,
,![]() 为椭圆
为椭圆![]() 的一个短轴顶点,
的一个短轴顶点,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若经过椭圆![]() 左焦点的直线
左焦点的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,
两点,![]() 为椭圆
为椭圆![]() 的右顶点,求
的右顶点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知球O是正三棱锥(底面为正三角形,顶点在底面的射影为底面中心)A-BCD的外接球,BC=3,![]() ,点E在线段BD上,且BD=3BE,过点E作圆O的截面,则所得截面圆面积的取值范围是__.
,点E在线段BD上,且BD=3BE,过点E作圆O的截面,则所得截面圆面积的取值范围是__.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=﹣x2+2|x|+1的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | ﹣2 |
| m | 2 | 1 | 2 | 1 |
| ﹣2 | … |
其中,m= .
(2)根据上表数据,在如图所示的平面直角坐标系中描点,画出了函数图象的一部分,请画出该函数图象的另一部分.
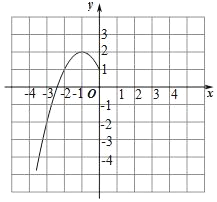
(3)观察函数图象,写出两条函数的性质./p>
(4)进一步探究函数图象发现:
①方程﹣x2+2|x|+1=0有 个实数根;
②关于x的方程﹣x2+2|x|+1=a有4个实数根时,a的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com