练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】边长分别为1， ，2 的三角形的最大角与最小角的和是（ ）
    A.90°
    B.120°
    C.135°
    D.150°

    【答案】C
    【解析】解：解法一：由题意可得，边长为1的边对的角最小为α，边长2 对的角最大为β，
    由余弦定理可得cosα= = = ，cosβ= =﹣ ，
    ∴sinα= ，sinβ= ，cos（α+β）=cosαcosβ﹣sinαsinβ=﹣ ﹣ =﹣ ，
    ∴α+β=135°，
    故选：C．
    解法二：由题意可得，边长为 的边对的角不是最大角、也不是最小角，设此角为θ，
    则由余弦定理可得cosθ= = ，∴θ=45°，
    故三角形的最大角与最小角的和是180°﹣45°=135°，
    故选：C．
    【考点精析】解答此题的关键在于理解余弦定理的定义的相关知识，掌握余弦定理:;;．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= ，
    （1）若a=﹣1，求f（x）的单调区间；
    （2）若f（x）有最大值3，求a的值．
    （3）若f（x）的值域是（0，+∞），求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，梯形ABEF中，AF∥BE，AB⊥AF，且AB=BC=AD=DF=2CE=2，沿DC将梯形DCFE折起，使得平面DCFE⊥平面ABCD．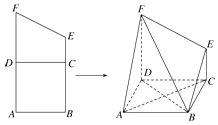
    （1）证明：AC∥平面BEF；
    （2）求三棱锥D﹣BEF的体积；
    （3）求直线AF与平面BDF所求的角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C的圆心在x轴上，点 在圆C上，圆心到直线2x﹣y=0的距离为 ，则圆C的方程为（ ）
    A.（x﹣2）2+y2=3
    B.（x+2）2+y2=9
    C.（x±2）2+y2=3
    D.（x±2）2+y2=9

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l经过直线l1：2x﹣y﹣1=0与直线l2：x+2y﹣3=0的交点P，且与直线l3：x﹣y+1=0垂直．
    （1）求直线l的方程；
    （2）若直线l与圆C：（x﹣a）2+y2=8相交于P，Q两点，且 ，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，A= ，cosB= ．
    （1）求cosC；
    （2）设BC= ，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆O：x2+y2=2，直线l：y=kx﹣2．
    （1）若直线l与圆O交于不同的两点A，B，且 ，求k的值；
    （2）若 ，P是直线l上的动点，过P作圆O的两条切线PC，PD，切点分别为C，D，求证：直线CD过定点，并求出该定点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料．生产一件产品A需要甲材料1.5kg，乙材料1kg，用5个工时；生产一件产品B需要甲材料0.5kg，乙材料0.3kg，用3个工时，生产一件产品A的利润为2100元，生产一件产品B的利润为900元．该企业现有甲材料150kg，乙材料90kg，则在不超过600个工时的条件下，生产产品A、产品B的利润之和的最大值为元．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C经过原点O，与x轴另一交点的横坐标为4，与y轴另一交点的纵坐标为2，
    （1）求圆C的方程；
    （2）已知点B的坐标为（0，2），设P，Q分别是直线l：x+y+2=0和圆C上的动点，求|PB|+|PQ|的最小值及此时点P的坐标．

    查看答案和解析>>

    同步练习册答案