练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】图是正方体的平面展开图，在这个正方体中：① 与 平行；② 与 是异面直线；③ 与 成 角；④ 与 垂直；以上四个命题中，正确的是（ ）

    A.①②③
    B.②④
    C.②③④
    D.③④

    【答案】D
    【解析】解：由已知中正方体的平面展开图，

    得到正方体的直观图如下图所示：

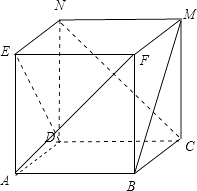
    由正方体的几何特征可得：

    ①BM与ED平行，不正确；

    ②CN与BE是异面直线，不正确，是平行线；

    ③AN∥BM，所以，CN与BM所成的角就是∠ANC=60°角，正确；

    ④DM与BN垂直，DM与BN垂直，正确；

    所以答案是：D．


    【考点精析】掌握异面直线及其所成的角和异面直线的判定是解答本题的根本，需要知道异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系；过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.（不在任何一个平面内的两条直线）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某某车站在春运期间为了改进服务，随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时，单位：min)．下面是这次抽样的频率分布表和频率分布直方图，解答下列问题：

    分组

    频数

    频率

    一组

    0≤t<5

    0

    0

    二组

    5≤t<10

    10

    三组

    10≤t<15

    10

    0.10

    四组

    15≤t<20

    五组

    20≤t<25

    30

    0.30

    合计

    100

    1.00

    (1)这次抽样的样本容量是多少？

    (2)在表中填写缺失的数据并补全频率分布直方图．

    (3)旅客购票用时的平均数可能落在哪一个小组？

    (4)若每增加一个购票窗口可使平均购票用时缩短5 min，要使平均购票用时不超过10 min，那么你估计最少要增加几个窗口？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从某居民区随机抽取10个家庭，获得第个家庭的月收入（单位：千元）与月储蓄（单位：千元）的数据资料，算得， ，

    ，

    (1).求家庭的月储蓄对月收入的线性回归方程；

    (2).判断变量与之间的正相关还是负相关；

    (3).若该居民区某家庭月收入为7千元，预测该家庭的月储蓄.

    附：回归直线的斜率和截距的最小二乘估计公式分别为

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数在区间上的最小值为.

    （1）求；

    （2）若在上恒成立，求实数的取值范围；

    （3）当 时，求满足的的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直三棱柱 中，底面 是边长为2的正三角形， 是棱 的中点，且 .

    （1）试在棱 上确定一点 ，使 平面 ；
    （2）当点 在棱 中点时，求直线 与平面 所成角的大小的正弦值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 在区间 上有最大值4和最小值1，
    设 ．
    （Ⅰ）求 的值；
    （Ⅱ）若不等式 在 上恒成立，求实数 的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将红、黑、蓝、白5张纸牌（其中白纸牌有2张）随机分发给甲、乙、丙、丁4个人，每人至少分得1张，则下列两个事件为互斥事件的是（ ）

    A. 事件“甲分得1张白牌”与事件“乙分得1张红牌”

    B. 事件“甲分得1张红牌”与事件“乙分得1张蓝牌”

    C. 事件“甲分得1张白牌”与事件“乙分得2张白牌”

    D. 事件“甲分得2张白牌”与事件“乙分得1张黑牌”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义：对于函数，若在定义域内存在实数，满足，则称为“局部奇函数”．

    （1）已知二次函数，试判断是否为定义域上的“局部奇函数”?若是，求出所有满足的的值；若不是，请说明事由．

    （2）若是定义在区间上的“局部奇函数”，求实数的取值范围．

    （3）若为定义域上的“局部奇函数”，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“奶茶妹妹”对某时间段的奶茶销售量及其价格进行调查，统计出售价x元和销售量y杯之间的一组数据如下表所示：

    价格x

    5

    5.5

    6.5

    7

    销售量y

    12

    10

    6

    4

    通过分析，发现销售量y对奶茶的价格x具有线性相关关系．
    （Ⅰ）求销售量y对奶茶的价格x的回归直线方程；
    （Ⅱ）欲使销售量为13杯，则价格应定为多少？
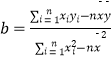    注：在回归直线y= 中， ， = ﹣ ． =146.5．

    查看答案和解析>>

    同步练习册答案