
【题目】已知直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的点,且
上的点,且![]() ,沿
,沿![]() 将
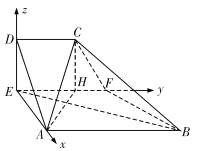
将![]() 折起并连接成如图的多面体
折起并连接成如图的多面体![]() ,折后
,折后![]() .
.
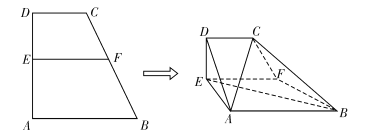
(Ⅰ)求证: ![]() ;
;
(Ⅱ)若折后直线![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦值是
的正弦值是![]() ,求证:平面
,求证:平面![]() 平面
平面![]() .
.
【答案】(Ⅰ)见解析;(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)由![]() ,
, ![]() 可得
可得![]() 平面
平面![]() ,从而
,从而![]() ,结合
,结合![]() ,根据线面垂直的判定定理可得;
,根据线面垂直的判定定理可得; ![]() 平面
平面![]() ,所以
,所以![]() ;(Ⅱ)作
;(Ⅱ)作![]() 于
于![]() ,连
,连![]() ,由(Ⅰ)知
,由(Ⅰ)知![]() ,即
,即![]() 为
为![]() 与平面
与平面![]() 所成角,设
所成角,设![]() ,
, ![]() ,而直线
,而直线![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]() ,即
,即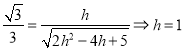 ,以
,以![]() 为轴建立坐标系,取
为轴建立坐标系,取![]() 的中点
的中点![]() ,先证明平面
,先证明平面![]() 的法向量是
的法向量是![]() ,再利用向量垂直数量积为零可得平面
,再利用向量垂直数量积为零可得平面![]() 的法向量,根据空间向量夹角的余弦公式可得结果.
的法向量,根据空间向量夹角的余弦公式可得结果.
试题解析:(Ⅰ)∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
又![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() ,
, ![]() ,
,
又![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() ,
, ![]() .
.
(Ⅱ)由(Ⅰ)知,可如图建立空间直角坐标系,
作![]() 于
于![]() ,连
,连![]() ,由(Ⅰ)知
,由(Ⅰ)知![]() ,
,
即![]() 为
为![]() 与平面
与平面![]() 所成角,设
所成角,设![]() ,
, ![]() ,
,
而直线![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]() ,即
,即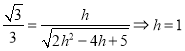 .
.
(或:平面![]() 的法向量是
的法向量是![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
则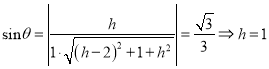 ).
).
易知平面![]() 平面
平面![]() 于
于![]() ,取
,取![]() 的中点
的中点![]() ,则
,则![]() 平面
平面![]() ,
,
而![]() ,则平面
,则平面![]() 的法向量是
的法向量是![]() ,
,
(或另法求出平面![]() 的法向量是
的法向量是![]() ),
),
再求出平面![]() 的法向量
的法向量![]() ,
,
设二面角![]() 是
是![]() ,则
,则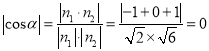 ,
,
∴平面![]() 平面
平面![]() .
.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,动点
中,动点![]() 到点
到点![]() 的距离和它到直线
的距离和它到直线![]() 的距离相等,记点
的距离相等,记点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求![]() 得方程;
得方程;
(Ⅱ)设点![]() 在曲线
在曲线![]() 上,
上, ![]() 轴上一点
轴上一点![]() (在点
(在点![]() 右侧)满足
右侧)满足![]() .平行于
.平行于![]() 的直线与曲线
的直线与曲线![]() 相切于点
相切于点![]() ,试判断直线
,试判断直线![]() 是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=1,a2=![]() ,an+1-
,an+1-![]() an+an-1=0 (n≥2,且n∈N*),若数列{an+1+λan}是等比数列.
an+an-1=0 (n≥2,且n∈N*),若数列{an+1+λan}是等比数列.
(1)求实数λ;
(2)求数列{an}的通项公式;
(3)设![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将边长为![]() 的正方形
的正方形![]() (及其内部)绕
(及其内部)绕![]() 旋转一周形成圆柱,如图,
旋转一周形成圆柱,如图, ![]() 长为
长为![]() ,
, ![]() 长为
长为![]() ,其中
,其中![]() 与
与![]() 在平面
在平面![]() 的同侧.
的同侧.
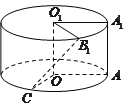
(1)求三棱锥![]() 的体积;
的体积;
(2)求异面直线![]() 与
与![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,设圆![]() :=4 cos 与直线l:=
:=4 cos 与直线l:=![]() (∈R)交于A,B两点.
(∈R)交于A,B两点.
(Ⅰ)求以AB为直径的圆![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)在圆![]() 任取一点
任取一点![]() ,在圆
,在圆![]() 上任取一点
上任取一点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
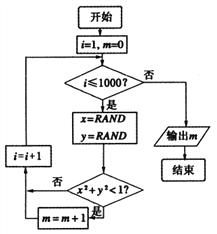
【题目】我们可以用随机模拟的方法估计![]() 的值,如图程序框图表示其基本步骤(函数
的值,如图程序框图表示其基本步骤(函数![]() 是产生随机数的函数,它能随机产生
是产生随机数的函数,它能随机产生![]() 内的任何一个实数).若输出的结果为
内的任何一个实数).若输出的结果为![]() ,则由此可估计
,则由此可估计![]() 的近似值为( )
的近似值为( )
A. 3.119 B. 3.124 C. 3.132 D. 3.151
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com