Question

【题目】《汉字听写大会》不断创收视新高，为了避免“书写危机”弘扬传统文化，某市对全市10万名市民进行了汉字听写测试，调查数据显示市民的成绩服从正态分布．现从某社区居民中随机抽取50名市民进行听写测试，发现被测试市民正确书写汉字的个数全部在160到184之间，将测试结果按如下方式分成六组：第一组，第二组，…，第六组，如图是按上述分组方法得到的频率分布直方图．

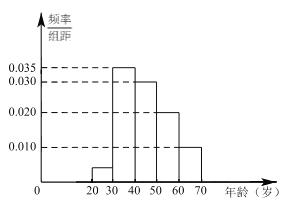
（1）若电视台记者要从抽取的市民中选1人进行采访，求被采访人恰好在第1组或第4组的概率；

（2）已知第1组市民中男性有3名，组织方要从第1组中随机抽取2名市民组成弘扬传统文化宣传队，求至少有1名女性群众的概率.

Answer 1

【答案】（Ⅰ）0.25；（Ⅱ） ．

【解析】试题分析：（Ⅰ）由频率分布直方图中所有小矩形的面积和为，求得第组频率值，再与第组频率求和，频率即为概率；（Ⅱ）先由频率求出第组的人组，可得其中男女各人，可列举出所有的基本事件，再找出其中含有女性的基本事件，利用古典概型可求得概率．．

试题解析：（Ⅰ）设第1组[20，30）的频率为f1，则由题意可知，

f1=1﹣（0.010+0.035+0.030+0.020）×10=0.05，

被采访人恰好在第1组或第4组的频率为(0.05+0.020)×10=0.25，

∴估计被采访人恰好在第1组或第4组的概率为0.25，

（Ⅱ）第1组[20，30）的人数为0.05×120=6，

∴第1组中共有6名市民，其中女性市民共3名，

记第1组中的3名男性市民分别为A，B，C，3名女性市民分别为x，y，z，

从第1组中随机抽取2名市民组成宣传队，共有15个基本事件，列举如下：AB，AC，Ax，Ay，Az，BC，Bx，By，Bz，Cx，Cy，Cz，xy，xz，yz，

至少有1名女性Ax，Ay，Az，Bx，By，Bz，Cx，Cy，Cz，xy，xz，yz共12个基本事件，∴从第1组中随机抽取2名市民组成宣传务队，至少有1名女性的概率为=．