
【题目】已知函数f(x)为R上的偶函数,g(x)为R上的奇函数,且f(x)+g(x)=log4(4x+1).
(1)求f(x),g(x)的解析式;
(2)若函数h(x)=f(x)﹣ ![]() 在R上只有一个零点,求实数a的取值范围.
在R上只有一个零点,求实数a的取值范围.
【答案】
(1)解:因为, ![]() …①,
…①,
∴ ![]() ,∴
,∴ ![]() …②
…②
由①②得, ![]() ,
, ![]()
(2)解:
由 ![]()
= ![]() .
.
得: ![]() ,
,
令t=2x,则t>0,即方程 ![]() …(*)只有一个大于0的根,
…(*)只有一个大于0的根,
①当a=1时, ![]() ,满足条件;
,满足条件;
②当方程(*)有一正一负两根时,满足条件,则 ![]() ,∴a>1,
,∴a>1,
③当方程(*)有两个相等的且为正的实根时,
则△=8a2+4(a﹣1)=0,∴ ![]() ,a=﹣1(舍)
,a=﹣1(舍) ![]() 时,
时, ![]() ,
,
综上: ![]() 或a≥1
或a≥1
【解析】(1)利用函数的奇偶性列出方程组求解即可得到函数的解析式.(2)利用函数只有一个零点,通过换元法,对a讨论,结合二次函数的性质求解即可.
【考点精析】解答此题的关键在于理解函数奇偶性的性质的相关知识,掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,为了测量对岸A,B两点的距离,沿河岸选取C,D两点,测得CD=2km,∠CDB=∠ADB=30°,∠ACD=60°,∠ACB=45°,求A,B两点的距离. 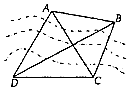
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的偶函数f(x)满足f(x+1)=﹣f(x),且当x∈[﹣1,0]时, ![]() ,函数
,函数 ![]() ,则关于x的不等式f(x)<g(x)的解集为( )
,则关于x的不等式f(x)<g(x)的解集为( )
A.(﹣2,﹣1)∪(﹣1,0)
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(﹣3)=0,则不等式f(x)g(x)<0的解集是( )
A.(﹣∞,﹣3)∪(0,3)
B.(﹣∞,﹣3)∪(3,+∞)
C.(﹣3,0)∪(3,+∞)
D.(﹣3,0)∪(0,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=2sin(2x+ ![]() )的图象为M,则下列结论中正确的是( )
)的图象为M,则下列结论中正确的是( )
A.图象M关于直线x=﹣ ![]() 对称
对称
B.由y=2sin2x的图象向左平移 ![]() 得到M
得到M
C.图象M关于点(﹣ ![]() ,0)对称
,0)对称
D.f(x)在区间(﹣ ![]() ,
, ![]() )上递增
)上递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={1,2},B={x|(x2+ax)(x2+ax+2)=0},记集合A中元素的个数为n(A),定义m(A,B)= ![]() ,若m(A,B)=1,则正实数a的值是 .
,若m(A,B)=1,则正实数a的值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|x﹣2a|+a2﹣4a(a∈R). (Ⅰ)当a=﹣1时,求f(x)在[﹣3,0]上的最大值和最小值;
(Ⅱ)若方程f(x)=0有3个不相等的实根x1 , x2 , x3 , 求 ![]() +
+ ![]() +
+ ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com