
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在极坐标系中,圆C的极坐标方程为:
为参数),在极坐标系中,圆C的极坐标方程为:![]()
(1)求圆C的直角坐标方程;
(2)设圆C与直线![]() 交于
交于![]() 两点,若点的坐标为
两点,若点的坐标为![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)利用极坐标公式把圆C的极坐标方程化为直角坐标方程.(2) 将l的参数方程代入圆C的直角坐标方程,得t2+2(cos α-sin α)t-7=0,利用弦长公式求出|PA|+|PB|=|t1|+|t2|=|t1-t2|=![]() ,再求其最小值.
,再求其最小值.
(1)由ρ=6sin θ得ρ2=6ρsin θ,化为直角坐标方程为x2+y2=6y,即x2+(y-3)2=9.
所以圆C的直角坐标方程为x2+(y-3)2=9.
(2)将l的参数方程代入圆C的直角坐标方程,得t2+2(cos α-sin α)t-7=0.
由已知得Δ=(2cos α-2sin α)2+4×7>0,
所以可设t1,t2是上述方程的两根,则![]()
由题意得直线l过点(1,2),结合t的几何意义得|PA|+|PB|=|t1|+|t2|=|t1-t2|
=![]() =
=![]() =
=![]() ≥
≥![]() =2
=2![]() .
.
所以|PA|+|PB|的最小值为2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
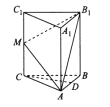
【题目】如图,在三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 是棱
是棱![]() 的中点,点
的中点,点![]() 在侧棱
在侧棱![]() 上运动.
上运动.
(1)当![]() 是棱
是棱![]() 的中点时,求证:
的中点时,求证: ![]() 平面
平面![]() ;
;
(2)当直线![]() 与平面
与平面![]() 所成的角的正切值为
所成的角的正切值为![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题,其中正确的命题序号是________.
①当![]() 时,函数
时,函数![]() 取得最大值,则
取得最大值,则![]()
②已知菱形![]() ,
,![]() 为
为![]() 的中点,且
的中点,且![]() ,则菱形
,则菱形![]() 面积的最大值为12
面积的最大值为12
③已知二次函数![]() ,如果
,如果![]() 时
时![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]()
④在三棱锥![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 的中点,则异面直线
的中点,则异面直线![]() 所成的角的余弦值是
所成的角的余弦值是![]()
⑤数列![]() 满足
满足![]() ,且数列
,且数列![]() 的前2010项的和为403,记数列
的前2010项的和为403,记数列![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,则
项和,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2-2x+1.
(1)试讨论函数f(x)的单调性;
(2)若![]() ≤a≤1,且f(x)在[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a),求g(a)的表达式;
≤a≤1,且f(x)在[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a),求g(a)的表达式;
(3)在(2)的条件下,求证:g(a)≥![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
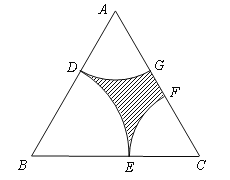
【题目】近年来,随着我市经济的快速发展,政府对民生越来越关注市区现有一块近似正三角形的土地![]() (如图所示),其边长为2百米,为了满足市民的休闲需求,市政府拟在三个顶点处分别修建扇形广场,即扇形
(如图所示),其边长为2百米,为了满足市民的休闲需求,市政府拟在三个顶点处分别修建扇形广场,即扇形![]() 和
和![]() ,其中
,其中![]() 与
与![]() 、
、![]() 分别相切于点
分别相切于点![]() ,且
,且![]() 与
与![]() 无重叠,剩余部分(阴影部分)种植草坪.设
无重叠,剩余部分(阴影部分)种植草坪.设![]() 长为
长为![]() (单位:百米),草坪面积为
(单位:百米),草坪面积为![]() (单位:万平方米).
(单位:万平方米).
(1)试用![]() 分别表示扇形
分别表示扇形![]() 和
和![]() 的面积,并写出
的面积,并写出![]() 的取值范围;
的取值范围;
(2)当![]() 为何值时,草坪面积最大?并求出最大面积.
为何值时,草坪面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点![]() 为圆心的圆过原点
为圆心的圆过原点![]() .
.
(1)设直线![]() 与圆
与圆![]() 交于点
交于点![]() ,若
,若![]() ,求圆
,求圆![]() 的方程;
的方程;
(2)在(1)的条件下,设![]() ,且
,且![]() 分别是直线
分别是直线![]() 和圆
和圆![]() 上的动点,求
上的动点,求![]() 的最大值及此时点
的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设三棱锥![]() 的底面是正三角形,侧棱长均相等,
的底面是正三角形,侧棱长均相等,![]() 是棱
是棱![]() 上的点(不含端点),记直线
上的点(不含端点),记直线![]() 与直线
与直线![]() 所成角为
所成角为![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,二面角
,二面角![]() 的平面角为
的平面角为![]() ,则( )
,则( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,PA垂直于⊙O所在的平面,M为圆周上任意一点,AN⊥PM,N为垂足.

(1)求证:AN⊥平面PBM;
(2)若AQ⊥PB,垂足为Q,求证:NQ⊥PB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com