
【题目】已知函数f(x)=x2﹣2lnx.
(1)求证:f(x)在(1,+∞)上单调递增.
(2)若f(x)≥2tx﹣ ![]() 在x∈(0,1]内恒成立,求实数t的取值范围.
在x∈(0,1]内恒成立,求实数t的取值范围.
【答案】
(1)解:证明:函数的定义域为(0,+∞),f′(x)=2x﹣ ![]() =
= ![]() ,
,
由f′(x)>0,得x>1,由f′(x)<0,得0<x<1,
所以,函数f(x)在区间(1,+∞)上单调递增
(2)解:由f(x)≥2tx﹣ ![]() 对x∈(0,1]恒成立,得2t≤x+
对x∈(0,1]恒成立,得2t≤x+ ![]() ﹣
﹣ ![]() .
.
令h(x)=x+ ![]() ﹣
﹣ ![]() ,则h′(x)=
,则h′(x)= ![]() ,
,
因为x∈(0,1],所以x4﹣3<0,﹣2x2<0,
2x2lnx<0,x4>0,
所以h′(x)<0,
所以h(x)在(0,1)上为减函数.
所以当x=1时,h(x)=h(x)=x+ ![]() ﹣
﹣ ![]() ,有最小值2,得2t≤2,
,有最小值2,得2t≤2,
所以t≤1,故t的取值范围是(﹣∞,1]
【解析】(1)先求函数的导数,根据导数和函数的单调性的关系即可求出,(2)要求若f(x)≥2tx﹣ ![]() 在x∈(0,1]内恒成立,即转化为2t≤x+
在x∈(0,1]内恒成立,即转化为2t≤x+ ![]() ﹣
﹣ ![]() 在x∈(0,1]内恒成立,只需求h(x)=x+
在x∈(0,1]内恒成立,只需求h(x)=x+ ![]() ﹣
﹣ ![]() x∈(0,1]内的最小值即可.
x∈(0,1]内的最小值即可.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知定义在实数集R上的函数f(x)满足f(1)=2,且f(x)的导数f'(x)在R上恒有f'(x)<1(x∈R),则不等式f(x)>x+1的解集为( )
A.(1,+∞)
B.(﹣∞,﹣1)∪(1,+∞)
C.(﹣1,1)
D.(﹣∞,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
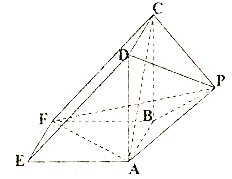
【题目】如图所示,该几何体是由一个直三棱柱![]() 和一个正四棱锥
和一个正四棱锥![]() 组合而成,
组合而成,![]() ,
,![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求正四棱锥![]() 的高
的高![]() ,使得该四棱锥的体积是三棱锥
,使得该四棱锥的体积是三棱锥![]() 体积的4倍.
体积的4倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos2 ![]() +
+ ![]() sinωx﹣
sinωx﹣ ![]() (ω>0),x∈R,若f(x)在区间(π,2π)内没有零点,则ω的取值范围是( )
(ω>0),x∈R,若f(x)在区间(π,2π)内没有零点,则ω的取值范围是( )
A.(0, ![]() ]
]
B.(0, ![]() ]∪[
]∪[ ![]() ,
, ![]() )
)
C.(0, ![]() ]
]
D.(0, ![]() ]∪[
]∪[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() +cos2x+a(a∈R,a为常数). (Ⅰ)求函数的最小正周期;
+cos2x+a(a∈R,a为常数). (Ⅰ)求函数的最小正周期;
(Ⅱ)求函数的单调递减区间;
(Ⅲ)若 ![]() 时,f(x)的最小值为﹣2,求a的值.
时,f(x)的最小值为﹣2,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|
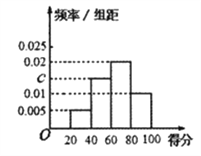
(Ⅰ)求![]() ,
, ![]() ,
, ![]() 的值;
的值;
(Ⅱ)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈.现再从这10人这任选4人,记所选4人的量化总分为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(Ⅲ)某评估机构以指标![]() (
(![]() ,其中
,其中![]() 表示
表示![]() 的方差)来评估该校安全教育活动的成效.若
的方差)来评估该校安全教育活动的成效.若![]() ,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(Ⅱ)的条件下,判断该校是否应调整安全教育方案?
,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(Ⅱ)的条件下,判断该校是否应调整安全教育方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)(x∈R)满足f(1)=1,且f(x)的导函数f′(x)≥ ![]() ,则f(x)<
,则f(x)< ![]() +
+ ![]() 的解集为( )
的解集为( )
A.{x|x<1}
B.{x|x>1}
C.{x|x<﹣1}
D.{x|x>﹣1}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com